练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，PA=PB，AD=DB，则（　　）
    A．PD?平面ABCB．PD⊥平面ABC
    C．PD与平面ABC相交但不垂直D．PD∥平面ABC

    分析 利用等腰三角形的性质可得：PD⊥AB，再利用面面垂直的性质定理即可得出．

    解答 解：∵PA=PB，AD=DB，∴PD⊥AB，
    又平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，
    ∴PD⊥平面ABC，
    因此B正确．
    故选：B．

    点评 本题考查了等腰三角形的性质、面面垂直的性质定理，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

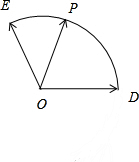    17．如图，若$\overrightarrow{a}$=$\overrightarrow{OD}$，$\overrightarrow{b}$=$\overrightarrow{OE}$，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°，|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，点P是以点O为圆心的圆弧$\widehat{DE}$上一动点，设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$（x，y∈R），求x+y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设点P为圆C1：x2+y2=2上的动点，过点P作x轴的垂线，垂足为Q，点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$．
    （1）求点M的轨迹C2的方程；
    （2）过直线x=2上的点T作圆C1的两条切线，设切点分别为A、B，若直线AB与（1）中的曲线C2交与C、D两点，求$\frac{{|{CD}|}}{{|{AB}|}}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．定点M（1，1），动A、B点在圆C：x2+y2=4上运动且MB垂直MA，则弦AB长度最小值为$\sqrt{6}$-$\sqrt{2}$．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知圆C：x2+y2-8x-4y+4=0及直线l：（2m+1）x+（m-1）y=7m-1（m∈R）．
    （1）证明：不论m取什么实数，直线l与圆C一定相交；
    （2）求直线l与圆C所截得的弦长的最短长度及此时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．若圆C：（x-$\frac{5}{2}$）2+（y-2）2=$\frac{25}{4}$上有4个点到直线x-y+a=0的距离为$\frac{1}{2}$，则实数a的取值范围为（$-\frac{1}{2}-2\sqrt{2}，-\frac{1}{2}+2\sqrt{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{3}}{3}$，以原点O为圆心，b为半径的圆与直线x-y+2=0相切，A、B分别是椭圆的左、右顶点，P为椭圆C上的动点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若P与A，B均不重合，直线PA，PB的斜率分别为k1，k2，求k1•k2的值；
    （Ⅲ）设M为过P且垂直于x轴的直线上的点，若$\frac{|OP|}{|OM|}$=λ（$\frac{\sqrt{3}}{3}$≤λ＜1），求点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设圆O：x2+y2=$\frac{16}{9}$，直线l：x+3y-8=0，点A∈l，圆O上存在点B且∠OAB=30°（O为坐标原点），则点A的纵坐标的取值范围[$\frac{32}{15}，\frac{8}{3}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．定积分${∫}_{-1}^{2}$|x2-1|dx=$\frac{8}{3}$．

    查看答案和解析>>

    同步练习册答案