
| A. | -1 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 若$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$与$\overrightarrow{b}$=-$\frac{1}{3}$$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$共线,则存在实数μ使得:$\overrightarrow{a}$=μ$\overrightarrow{b}$,即$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$=μ(-$\frac{1}{3}$$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$),根据平面向量的基本定理,可得答案.
解答 解:∵$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{1}}$是两个不共线的向量,
若$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$与$\overrightarrow{b}$=-$\frac{1}{3}$$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$共线,
则存在实数μ使得:$\overrightarrow{a}$=μ$\overrightarrow{b}$,即$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$=μ(-$\frac{1}{3}$$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$),
即$\left\{\begin{array}{l}{1=-μ}\\{λ=-\frac{1}{3}μ}\end{array}\right.$,解得:λ=$\frac{1}{3}$,
故选:D
点评 本题考查的知识点是平面向量的基本定义,向量共线定理,方程思想,难度中档.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
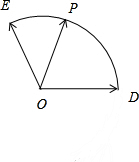 如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.
如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com