
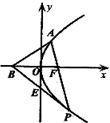
 已知抛物线C:y2=2px(p≠0)的焦点F在直线2x+y-2=0上.
已知抛物线C:y2=2px(p≠0)的焦点F在直线2x+y-2=0上.分析 (1)抛物线C的焦点$F(\frac{p}{2},0)$在x轴上,求出p=2.由此能求出抛物线C的方程.
(2)由点P是C上异于坐标原点O的任意一点,设$P(\frac{t^2}{4},t)(t≠0)$.设切线BP的方程为$y-t=k(x-\frac{t^2}{4})$.由$\left\{\begin{array}{l}y-t=k(x-\frac{t^2}{4})\\{y^2}=4x\end{array}\right.$,得:ky2-4y-kt2+4t=0,由此利用根的判别式、切线方程,结合已知条件能证明λ为定值.
(3)设直线FP的方程为x=my+1,由$\left\{\begin{array}{l}x=my+1\\{y^2}=4x\end{array}\right.$,得:$\frac{y^2}{4}-my-1=0$,由此利用韦达定理、弦长公式得到S△PAB=$\frac{1}{8}×(4+{t^2})×|\frac{4}{t}+t|$,令$f(t)=\frac{1}{8}(4+{t^2})×|\frac{4}{t}+t|(t≠0)$,则f(t)为偶函数,只需研究函数f(t)在t>0时的最小值即可.利用导数性质能求出结果.
解答 解:(1)由题意,抛物线C的焦点$F(\frac{p}{2},0)$在x轴上.…(1分)
在方程2x+y-2=0中,令y=0,得x=1.…(2分)
于是,$\frac{p}{2}=1$.解得p=2.
所以,抛物线C的方程为y2=4x.…(3分)
证明:(2)由点P是C上异于坐标原点O的任意一点,设$P(\frac{t^2}{4},t)(t≠0)$.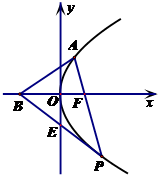 设切线BP的斜率为k,则切线BP的方程为$y-t=k(x-\frac{t^2}{4})$.
设切线BP的斜率为k,则切线BP的方程为$y-t=k(x-\frac{t^2}{4})$.
由$\left\{\begin{array}{l}y-t=k(x-\frac{t^2}{4})\\{y^2}=4x\end{array}\right.$,消去x并整理得:ky2-4y-kt2+4t=0.…(4分)
由k≠0,考虑到判别式△=16-4k(-kt2+4t)=0.
可得4(kt-2)2=0.所以kt-2=0.故切线BP的斜率$k=\frac{2}{t}$.…(5分)
切线BP的方程为$y-t=\frac{2}{t}(x-\frac{t^2}{4})$,即$y=\frac{2}{t}x+\frac{t}{2}$.
在$y=\frac{2}{t}x+\frac{t}{2}$中,令x=0,得$y=\frac{t}{2}$.所以点E的坐标为$(0,\frac{t}{2})$;
在$y=\frac{2}{t}x+\frac{t}{2}$中,令y=0,得$x=-\frac{t^2}{4}$.所以点B的坐标为$(-\frac{t^2}{4},0)$.…(7分)
所以$\overrightarrow{PE}=(0,\frac{t}{2})-(\frac{t^2}{4},t)=(-\frac{t^2}{4},-\frac{t}{2})$,$\overrightarrow{PB}=(-\frac{t^2}{4},0)-(\frac{t^2}{4},t)=(-\frac{t^2}{2},-t)$.
所以$\overrightarrow{PE}=\frac{1}{2}\overrightarrow{PB}$.故$λ=\frac{1}{2}$,为定值.…(8分)
解:(3)由直线FP过点F(1,0),
设直线FP的方程为x=my+1.
由$\left\{\begin{array}{l}x=my+1\\{y^2}=4x\end{array}\right.$,消去x得:$\frac{y^2}{4}-my-1=0$.
由韦达定理,得yAyP=-4.所以${y_A}_{\;}=-\frac{4}{y_P}=-\frac{4}{t}$.…(9分)
于是${S_{△PAB}}=\frac{1}{2}×|BF|×|{y_A}-{y_P}|=\frac{1}{2}×(1+\frac{t^2}{4})×|-\frac{4}{t}-t|$=$\frac{1}{8}×(4+{t^2})×|\frac{4}{t}+t|$…(10分)
令$f(t)=\frac{1}{8}(4+{t^2})×|\frac{4}{t}+t|(t≠0)$,则f(t)为偶函数,只需研究函数f(t)在t>0时的最小值即可.
当t>0时,$f(t)=\frac{1}{8}(4+{t^2})×(\frac{4}{t}+t)=\frac{1}{8}({t^3}+8t+\frac{16}{t})$,
$f'(t)=\frac{1}{8}(3{t^2}+8-\frac{16}{t^2})=\frac{1}{{8{t^2}}}(3{t^4}+8{t^2}-16)=\frac{1}{{8{t^2}}}(3{t^2}-4)({t^2}+4)$.
当$0<t<\frac{2}{{\sqrt{3}}}$时,f'(t)<0,f(t)为减函数;
当$t>\frac{2}{{\sqrt{3}}}$时,f'(t)>0,f(t)为增函数.…(11分)
所以,当t>0时,函数f(t)在$t=\frac{2}{{\sqrt{3}}}$时取最小值$f(\frac{2}{{\sqrt{3}}})=\frac{{16\sqrt{3}}}{9}$.
因为f(t)为偶函数,当t<0时,函数f(t)在$t=-\frac{2}{{\sqrt{3}}}$时取最小值$f(-\frac{2}{{\sqrt{3}}})=\frac{{16\sqrt{3}}}{9}$.…(12分)
当$t=\frac{2}{{\sqrt{3}}}$时,点P的坐标为$(\frac{1}{3},\frac{2}{{\sqrt{3}}})$;当$t=-\frac{2}{{\sqrt{3}}}$时,点P的坐标为$(\frac{1}{3},-\frac{2}{{\sqrt{3}}})$.
综上,△PAB的面积存在最小值$\frac{{16\sqrt{3}}}{9}$,
此时点P的坐标为$(\frac{1}{3},\frac{2}{{\sqrt{3}}})$或$(\frac{1}{3},-\frac{2}{{\sqrt{3}}})$.…(13分)
点评 本题考查抛物线方程的求法,考查实数为定值的证明,考查三角形面积能否存在最小值的判断与求法,是中档题,解题时要认真审题,注意根的判别式、切线方程、韦达定理、弦长公式、导数性质的合理运用.


科目:高中数学 来源: 题型:解答题
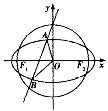 如图,以${{F}_1}({-\sqrt{3},0})$、${{F}_2}({\sqrt{3},0})$为焦点的椭圆C与以原点O为圆心,F1F2为直径的圆在第一象限的交点的纵坐标为$\frac{{\sqrt{3}}}{3}$.
如图,以${{F}_1}({-\sqrt{3},0})$、${{F}_2}({\sqrt{3},0})$为焦点的椭圆C与以原点O为圆心,F1F2为直径的圆在第一象限的交点的纵坐标为$\frac{{\sqrt{3}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知点P是圆锥母线SA的中点,Q是底面圆周上的点,M是线段PQ的中点,当点Q在圆周上运动一周时,点M的轨迹是( )
如图,已知点P是圆锥母线SA的中点,Q是底面圆周上的点,M是线段PQ的中点,当点Q在圆周上运动一周时,点M的轨迹是( )| A. | 线段 | B. | 圆 | C. | 椭圆 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{2}$,5) | B. | [$\frac{3}{2}$,3] | C. | [3,5) | D. | [3,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com