
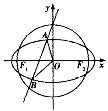
 如图,以${{F}_1}({-\sqrt{3},0})$、${{F}_2}({\sqrt{3},0})$为焦点的椭圆C与以原点O为圆心,F1F2为直径的圆在第一象限的交点的纵坐标为$\frac{{\sqrt{3}}}{3}$.
如图,以${{F}_1}({-\sqrt{3},0})$、${{F}_2}({\sqrt{3},0})$为焦点的椭圆C与以原点O为圆心,F1F2为直径的圆在第一象限的交点的纵坐标为$\frac{{\sqrt{3}}}{3}$.分析 (1)利用圆的方程及已知条件求出椭圆与圆的一个交点坐标,代入椭圆方程,结合椭圆的焦点坐标即可求出椭圆的标准方程.
(2)联立直线与椭圆的方程,利用弦长公式表示出|AB|,利用点到直线的距离公式表示出O到AB的距离,从而得到△OAB面积的表达式(用k表示),再解不等式即可得到直线l的斜率k的取值范围.
解答 解:(1)由题意知,圆的方程为x2+y2=3,则椭圆C与圆在第一象限的交点坐标为($\frac{2\sqrt{6}}{5}$,$\frac{\sqrt{3}}{3}$).
设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
则$\left\{\begin{array}{l}{{a}^{2}={b}^{2}+{c}^{2}}\\{c=\sqrt{3}}\end{array}\right.$,①
又点($\frac{2\sqrt{6}}{5}$,$\frac{\sqrt{3}}{3}$)在椭圆上,∴$\frac{(\frac{2\sqrt{6}}{3})^{2}}{{a}^{2}}$+$\frac{(\frac{\sqrt{3}}{3})^{2}}{{b}^{2}}$=1,②
联立①②解得a=2,b=1,
故椭圆C的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)由(1)知,圆x2+y2=3与y轴正半轴的交点坐标为(0,$\sqrt{3}$),
由题意知直线l的斜率k不存在时,△OAB不存在;
设A(x1,y1),B(x2,y2),直线l的方程为y=kx+$\sqrt{3}$,
代入$\frac{{x}^{2}}{4}+$y2=1,得(1+4k2)x2+8$\sqrt{3}$kx+8=0,
则△=(8$\sqrt{3}$k)2-4×8(1+4k2)>0,即k2>$\frac{1}{2}$,x1+x2=$\frac{8\sqrt{3}k}{1+4{k}^{2}}$,x1•x2=$\frac{8}{1+4{k}^{2}}$.
∴|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$
=$\sqrt{(1+{k}^{2})[(-\frac{8\sqrt{3}k}{1+4{k}^{2}})^{2}-4×\frac{8}{1+4{k}^{2}}]}$
=$\frac{4\sqrt{(1+{k}^{2})(4{k}^{2}-2)}}{1+4{k}^{2}}$,
又点O到直线l的距离d=$\frac{\sqrt{3}}{\sqrt{1+{k}^{2}}}$,
∴△OAB的面积S=$\frac{1}{2}$×$\frac{4\sqrt{(1+{k}^{2})(4{k}^{2}-2)}}{1+4{k}^{2}}$×$\frac{\sqrt{3}}{\sqrt{1+{k}^{2}}}$=$\frac{2\sqrt{6}×\sqrt{2{k}^{2}-1}}{1+4{k}^{2}}$≥$\frac{2\sqrt{6}}{5}$,
解得1≤k2≤$\frac{13}{8}$,即-$\frac{\sqrt{26}}{4}$≤k≤-1或1≤k≤$\frac{\sqrt{26}}{4}$.
故所求直线l的斜率k的取值范围为[-$\frac{\sqrt{26}}{4}$,-1]∪[1,$\frac{\sqrt{26}}{4}$].
点评 本题考查椭圆的几何性质、直线与椭圆的位置关系,直线和圆锥曲线的位置关系多涉及位置关系的判断,直线被曲线截得的弦长、三角形的面积、向量的数量积等有关最值或取值范围的问题.解析几何中的探究性问题以定点、定直线、定值的存在性问题为主,多以直线经过定点、直线和圆相切以及有关图形的面积等问题为主,圆锥曲线和圆相结合、多种圆锥曲线相结合的问题,尤其是椭圆、抛物线与圆相结合将会成为今后高考命题的趋势.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 一矩形的一边在x轴上,另两个顶点在函数y=$\frac{x}{{1+{x^2}}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
一矩形的一边在x轴上,另两个顶点在函数y=$\frac{x}{{1+{x^2}}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
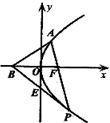 已知抛物线C:y2=2px(p≠0)的焦点F在直线2x+y-2=0上.
已知抛物线C:y2=2px(p≠0)的焦点F在直线2x+y-2=0上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com