
分析 首先对函数变形为ax+$\frac{b}{x}$(a>0,b>0)的形式,根据基本不等式得到函数的单调性,进一步求最小值.
解答 解:函数f(x)=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$=$\sqrt{{x}^{2}+2}+\frac{1}{\sqrt{{x}^{2}+2}}$,
因t=$\sqrt{{x}^{2}+2}≥$2,所以函数f(x)=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$为f(t)=t+$\frac{1}{t}$在t≥2为增函数,所以f(t)≥$\frac{3\sqrt{2}}{2}$;
此时t=2即x=0.
点评 本题变形后容易利用基本不等式求最小值,而忽略基本不等式成立的三个条件;即本题利用基本不等式求最小值时,等号不成立.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinA | B. | cosB | C. | tanA | D. | cotA |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
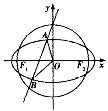 如图,以${{F}_1}({-\sqrt{3},0})$、${{F}_2}({\sqrt{3},0})$为焦点的椭圆C与以原点O为圆心,F1F2为直径的圆在第一象限的交点的纵坐标为$\frac{{\sqrt{3}}}{3}$.
如图,以${{F}_1}({-\sqrt{3},0})$、${{F}_2}({\sqrt{3},0})$为焦点的椭圆C与以原点O为圆心,F1F2为直径的圆在第一象限的交点的纵坐标为$\frac{{\sqrt{3}}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com