
分析 对n分类讨论,利用数列的单调性与一元二次不等式的解法即可得出.
解答 解:bn=$\frac{n-2}{{2}^{n}}$,
可得:b1=-$\frac{1}{2}$,b2=0,b3=$\frac{1}{8}$,
n≥3时,bn>0,bn+1-bn=$\frac{n-1}{{2}^{n+1}}$-$\frac{n-2}{{2}^{n}}$=$\frac{3-n}{{2}^{n+1}}$
∴n=3时,b3=b4,n≥4时,bn+1<bn,此时数列{bn}单调递减,
因此n=3或4时,bn取得最大值$\frac{1}{8}$,
∵对任意的n∈N*,都有$\frac{7}{8}$+bn≤t2恒成立,
∴$\frac{7}{8}$+$\frac{1}{8}$≤t2,
∴t≤-1或t≥1,
故t的取值范围为(-∞,-1]∪[1,+∞)
点评 本题考查了数列的单调性与一元二次不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
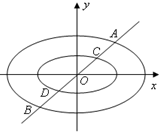 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1.
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曲线E上的所有点都是“好点” | |
| B. | 曲线E上仅有有限个点是“好点” | |
| C. | 曲线E上的所有点都不是“好点” | |
| D. | 曲线E上有无穷多个点(但不是所有的点)是“好点” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
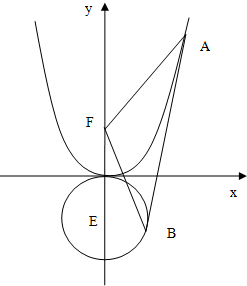 已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)
已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知点P是圆锥母线SA的中点,Q是底面圆周上的点,M是线段PQ的中点,当点Q在圆周上运动一周时,点M的轨迹是( )
如图,已知点P是圆锥母线SA的中点,Q是底面圆周上的点,M是线段PQ的中点,当点Q在圆周上运动一周时,点M的轨迹是( )| A. | 线段 | B. | 圆 | C. | 椭圆 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com