
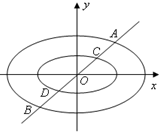
 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1.
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1.分析 (1)由题意椭圆C2与C1相似,由椭圆C2的特征三角形是腰长为4,底边长为4$\sqrt{3}$的等腰三角形,能求出C2与C1的相似比.
(2)椭圆Cb的方程为:$\frac{{x}^{2}}{4{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(b>0),设直线lMN:y=-x+t,点M(x1,y1),N(x2,y2),MN中点为(x0,y0),由$\left\{\begin{array}{l}{y=-x+t}\\{\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,得5x2-8tx+4(t2-b2)=0,由此利用韦达定理、根的判别式能求出实数b的取值范围.
(3)法1:过原点作直线y=kx(k≠1),交椭圆M和椭圆M1于点E和点F,得到△CDF和△ABE即为所求相似三角形,且相似比为λ.
法2:过点A、点C分别做x轴(或y轴)的垂线,交椭圆M和椭圆M1点E和点F,得到△CDF和△ABE即为所求相似三角形,且相似比为λ.
解答 解:(1)椭圆C2与C1相似.…(2分)
因为椭圆C2的特征三角形是腰长为4,底边长为4$\sqrt{3}$的等腰三角形,
而椭圆C1的特征三角形是腰长为2,底边长为2$\sqrt{3}$的等腰三角形,
因此两个等腰三角形相似,且相似比为2:1.…(5分)
(2)椭圆Cb的方程为:$\frac{{x}^{2}}{4{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(b>0),…(6分)
设直线lMN:y=-x+t,点M(x1,y1),N(x2,y2),MN中点为(x0,y0),
则$\left\{\begin{array}{l}{y=-x+t}\\{\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,∴5x2-8tx+4(t2-b2)=0,
则${x}_{0}=\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{4t}{5}$,${y}_{0}=\frac{t}{5}$,…(8分)
∵中点在直线y=x+1上,∴$\frac{t}{5}=\frac{4t}{5}+1$,t=-$\frac{5}{3}$,…(10分)
即直线lMN的方程为:${l}_{MN}:y=-x-\frac{5}{3}$,
由题意可知,直线lMN与椭圆Cb有两个不同的交点,
即方程$5{x}^{2}-8(-\frac{5}{3})x+4[(-\frac{5}{3})^{2}-{b}^{2}]=0$有两个不同的实数解,
∴△=($\frac{40}{3}$)2-4×5×4×($\frac{25}{9}$-b2)>0,即b>$\frac{\sqrt{5}}{3}$.…(13分)
(3)作法1:过原点作直线y=kx(k≠1),交椭圆M和椭圆M1于点E和点F,
则△CDF和△ABE即为所求相似三角形,且相似比为λ.…(18分)
作法2:过点A、点C分别做x轴(或y轴)的垂线,交椭圆M和椭圆M1点E和点F,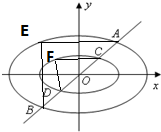
则△CDF和△ABE即为所求相似三角形,且相似比为λ.…(18分)
点评 本题考查两个椭圆是否相似的判断与相似比的求法,考查实数的取值范围的求法,考查满足条件的点的作法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题

| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一矩形的一边在x轴上,另两个顶点在函数y=$\frac{x}{{1+{x^2}}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
一矩形的一边在x轴上,另两个顶点在函数y=$\frac{x}{{1+{x^2}}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E
已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com