练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．某几何体的三视图如图所示（均由边长为$\sqrt{2}$的正方形及其对角线组成），则该几何体的表面积为（　　）
    A．8$\sqrt{3}$B．4$\sqrt{3}$C．8$\sqrt{2}$D．4$\sqrt{2}$

    分析 如图所示，该几何体是同底面的上下两个正四棱锥．

    解答 解：如图所示，该几何体是同底面的上下两个正四棱锥．
    则该几何体的表面积S=8×$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{{1}^{2}+（\frac{\sqrt{2}}{2}）^{2}}$=4$\sqrt{3}$．
    故选：B．

    点评 本题考查了正八面体的三视图及其表面积计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．从某地高中男生中随机抽取100名同学，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．若要从身高在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取6人参加一项活动，再从这6人选两人当正负队长，则这两人体重不在同一组内的概率为$\frac{11}{15}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知四面体P-ABC的外接球的球心O在AB上，且PO⊥平面ABC，AB=2AC，若四面体P一ABC的体积为$\frac{9\sqrt{3}}{16}$，则该球的表面积为9π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若正三棱柱的所有棱长均为a，且其体积为2$\sqrt{3}$，则此三棱柱外接球的表面积是（　　）
    A．$\frac{8}{3}$πB．$\frac{28}{3}$πC．3πD．$\frac{4}{3}$π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知动点M（x，y）在过点（-$\frac{3}{2}$，-2）的圆x2+y2-2x+4y=0的两条切线和x-y+1=0围成的区域内，则$\frac{x+1}{x+2y-3}$的取值范围为（　　）
    A．（-1，0）∪（0，$\frac{1}{7}$]B．[-1，0）∪（0，$\frac{1}{7}$]C．[-1，0）∪（0，$\frac{1}{7}$）D．[-1，$\frac{1}{7}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知长方体形的铜块长、宽、高分别是2，4，8，将它熔化后铸成一个正方体形的铜块（不计损耗），求铸成的铜块的棱长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若函数f（x）=eax-$\frac{lnx}{a}$（a＞0）存在零点，则a的取值范围是（　　）
    A．（0，$\frac{1}{e}$]B．（0，$\frac{1}{{e}^{2}}$]C．[$\frac{1}{{e}^{2}}$，$\frac{1}{e}$]D．[$\frac{1}{e}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．函数 y=f（x）的反函数为y=log2x，则 f（-1）=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

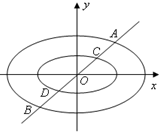    3．定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆C1：$\frac{{x}^{2}}{4}$+y2=1．
    （1）若椭圆C2：$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
    （2）写出与椭圆C1相似且焦点在x轴上、短半轴长为b的椭圆Cb的标准方程；若在椭圆Cb上存在两点M、N关于直线y=x+1对称，求实数b的取值范围；
    （3）如图：直线y=x与两个“相似椭圆”M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和
    Mλ：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=λ2（a＞bo，0＜λ＜1）分别交于点A，B和点C，D，试在椭圆M和椭圆Mλ上分别作出点E和点F（非椭圆顶点），使△CDF和△ABE组成以λ为相似比的两个相似三角形，写出具体作法．（不必证明）

    查看答案和解析>>

    同步练习册答案