
| A. | (0,$\frac{1}{e}$] | B. | (0,$\frac{1}{{e}^{2}}$] | C. | [$\frac{1}{{e}^{2}}$,$\frac{1}{e}$] | D. | [$\frac{1}{e}$,+∞) |
分析 先考虑函数f(x)=ax与g(x)=logax(a>1)图象仅有一个交点,且在公共点处有公共的切线,a的值,再利用换元法,即可得出结论.
解答 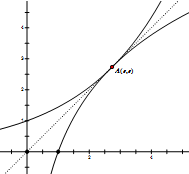 解:先考虑函数f(x)=ax与g(x)=logax(a>1)图象仅有一个交点,且在公共点处有公共的切线,a的值.
解:先考虑函数f(x)=ax与g(x)=logax(a>1)图象仅有一个交点,且在公共点处有公共的切线,a的值.
两函数互为反函数,则该切线即为y=x,设切点A,
可求出A(e,e),此时a=${e}^{\frac{1}{a}}$.
若a>${e}^{\frac{1}{a}}$时,则f(x)=ax与g(x)=logax(a>1)无公共点;
若1<a<${e}^{\frac{1}{a}}$时,则f(x)=ax与g(x)=logax(a>1)有两个公共点.
对f(x)=eax-$\frac{lnx}{a}$(a>0),换元令t=ea,即得tx=logtx,
由上知ea=t≤${e}^{\frac{1}{a}}$,得a≤$\frac{1}{e}$.
故选A.
点评 本题考查函数的零点,考查数形结合的数学思想,考查学生转化问题的能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,3) | B. | [-1,3) | C. | (-1,3) | D. | (-3,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{7}$,-1) | B. | (-$\sqrt{7}$,-1] | C. | (-$\sqrt{7}$,-2) | D. | (-$\sqrt{7}$,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com