
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 根据集合关系得到P?Q,然后根据四种命题真假关系进行判断即可.
解答 解:P={x|x=k+$\frac{1}{2}$,k∈z}={x|x=$\frac{2k+1}{2}$,k∈z},Q={x|x=$\frac{k}{2}$,k∈z},
则P?Q,
则原命题:“x∈P,则x∈Q”为真命题.,则命题的逆否命题为真命题,
命题的逆命题为:“x∈Q,则x∈P”,为假命题,
当x=$\frac{2}{2}$=1时,x∈Q,但x∈P不成立,即逆命题为假命题,则命题的否命题也是假命题,
故四种命题中真命题的个数为2个,
故选:C
点评 本题主要考查四种命题之间的关系的应用,根据逆否命题的等价性只需要判断两个命题的真假性是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$] | B. | (0,$\frac{1}{{e}^{2}}$] | C. | [$\frac{1}{{e}^{2}}$,$\frac{1}{e}$] | D. | [$\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
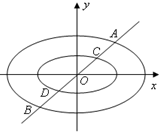 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1.
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知点P是圆锥母线SA的中点,Q是底面圆周上的点,M是线段PQ的中点,当点Q在圆周上运动一周时,点M的轨迹是( )
如图,已知点P是圆锥母线SA的中点,Q是底面圆周上的点,M是线段PQ的中点,当点Q在圆周上运动一周时,点M的轨迹是( )| A. | 线段 | B. | 圆 | C. | 椭圆 | D. | 抛物线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com