
���� ��1���ɡ�ABF1���ܳ�Ϊ4$\sqrt{2}$��������Ϊ$\frac{\sqrt{2}}{2}$�����a��b���ɴ��������ԲC�ı����̣�
��2����ֱ��l�ķ���Ϊy=kx-1��������Բ���̣��ã�2+k2��x2-2kx-1=0���ɴ�����Τ�ﶨ�����ҳ���ʽ����Ԫ���������֪���������ƽ���ı���PAQB�Խ���PQ�ij��ȵ�ȡֵ��Χ��
��� �⣺��1���ߡ�ABF1���ܳ�Ϊ4$\sqrt{2}$����4a=4$\sqrt{2}$��
���a=$\sqrt{2}$��
��e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����c=1����b=$\sqrt{2-1}$=1��
����ԲC�ı�����Ϊ${x}^{2}+\frac{{y}^{2}}{2}$=1��
��2����A��x1��y1����B��x2��y2����AB�е�E��x0��y0����
��ֱ��б�ʲ�����ʱ��������
����ֱ��l�ķ���Ϊy=kx-1����
���ٴ�����Բ����${x}^{2}+\frac{{y}^{2}}{2}$=1�������ã���2+k2��x2-2kx-1=0��
��${x}_{1}+{x}_{2}=\frac{2k}{2+{k}^{2}}$��${x}_{1}{x}_{2}=\frac{-1}{2+{k}^{2}}$��
${x}_{0}=\frac{k}{2+{k}^{2}}$��${y}_{0}=k•{x}_{0}-1=\frac{-2}{2+{k}^{2}}$��
|PE|=$\sqrt{��{x}_{0}-0��^{2}+��{y}_{0}+2��^{2}}$
=$\sqrt{��\frac{k}{2+{k}^{2}}��^{2}+��2-\frac{2}{2+{k}^{2}}��^{2}}$
=$\sqrt{\frac{{k}^{2}}{��2+{k}^{2}��^{2}}+\frac{4��1+{k}^{2}��^{2}}{��2+{k}^{2}��^{2}}}$��
��t=2+k2����t��[2��+�ޣ�����$\frac{1}{t}$�ʣ�0��$\frac{1}{2}$]��
��|PE|=$\sqrt{\frac{t-2+4��t-1��^{2}}{{t}^{2}}}$=$\sqrt{\frac{4{t}^{2}-7t+2}{{t}^{2}}}$=$\sqrt{\frac{2}{{t}^{2}}-\frac{7}{t}+4}$=$\sqrt{2��\frac{1}{t}-\frac{7}{4}��^{2}-\frac{17}{8}}$��[1��2����
��ƽ���ı���PAQB�Խ���PQ�ij��ȵ�ȡֵ��Χ��[1��2����
���� ���⿼����Բ���̵�������ƽ���ı��ζԽ��ߵij��ȵ�ȡֵ��Χ�������е��⣬����ʱҪ�������⣬ע��Τ�ﶨ�����ҳ���ʽ����Ԫ������Բ���ʵĺ������ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
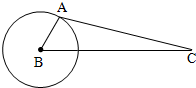 ͨѶ����C�ڳ���Ͽ�3R��RΪ����뾶���Ĺ���ϣ���ÿ24Сʱ�Ƶ���һ�ܣ���������λ�ڳ����ijһ����Ͽգ�����˵���ij��A����γ60�㣩��ͬһ���������ߣ�����A�۲�����ǵ����ǵ�����ֵΪ$\frac{3}{6}$��
ͨѶ����C�ڳ���Ͽ�3R��RΪ����뾶���Ĺ���ϣ���ÿ24Сʱ�Ƶ���һ�ܣ���������λ�ڳ����ijһ����Ͽգ�����˵���ij��A����γ60�㣩��ͬһ���������ߣ�����A�۲�����ǵ����ǵ�����ֵΪ$\frac{3}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
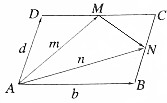 ��ͼ��ʾ��ƽ���ı���ABCD�У�MΪDC���е㣬N��BC���е㣬��$\overrightarrow{AB}$=$\overrightarrow{b}$��$\overrightarrow{AD}$=$\overrightarrow{d}$��$\overrightarrow{AM}$=$\overrightarrow{m}$��$\overrightarrow{AN}$=$\overrightarrow{n}$��
��ͼ��ʾ��ƽ���ı���ABCD�У�MΪDC���е㣬N��BC���е㣬��$\overrightarrow{AB}$=$\overrightarrow{b}$��$\overrightarrow{AD}$=$\overrightarrow{d}$��$\overrightarrow{AM}$=$\overrightarrow{m}$��$\overrightarrow{AN}$=$\overrightarrow{n}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com