
【题目】已知A,B,C为锐角△ABC的内角, ![]() =(sinA,sinBsinC),
=(sinA,sinBsinC), ![]() =(1,﹣2),
=(1,﹣2), ![]() ⊥
⊥ ![]() .
.
(1)tanB,tanBtanC,tanC能否构成等差数列?并证明你的结论;
(2)求tanAtanBtanC的最小值.
【答案】
(1)解:依题意有sinA=2sinBsinC.
在△ABC中,A=π﹣B﹣C,
所以sinA=sin(B+C)=sinBcosC+cosBsinC,
所以2sinBsinC=sinBcosC+cosBsinC.
因为△ABC为锐角三角形,所以cosB>0,cosC>0,
所以tanB+tanC=2tanBtanC,
所以tanB,tanBtanC,tanC成等差数列.
(2)解:在锐角△ABC中,
tanA=tan(π﹣B﹣C)=﹣tan(B+C)=﹣ ![]() ,
,
即tanAtanBtanC=tanA+tanB+tanC,
由(1)知tanB+tanC=2tanBtanC,
于是tanAtanBtanC=tanA+2tanBtanC≥ ![]() ,
,
整理得tanAtanBtanC≥8,
当且仅当tanA=4时取等号,
故tanAtanBtanC的最小值为8.
【解析】(1)依题意有sinA=2sinBsinC,从而2sinBsinC=sinBcosC+cosBsinC,再由cosB>0,cosC>0,能推导出tanB,tanBtanC,tanC成等差数列.(2)推导出tanAtanBtanC=tanA+tanB+tanC,从而tanAtanBtanC≥8,由此能求出tanAtanBtanC的最小值为8.
【考点精析】解答此题的关键在于理解数量积判断两个平面向量的垂直关系的相关知识,掌握若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直.
两平面的法向量垂直.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图为四棱锥P﹣ABCD的表面展开图,四边形ABCD为矩形, ![]() ,AD=1.已知顶点P在底面ABCD上的射影为点A,四棱锥的高为
,AD=1.已知顶点P在底面ABCD上的射影为点A,四棱锥的高为 ![]() ,则在四棱锥P﹣ABCD中,PC与平面ABCD所成角的正切值为 .
,则在四棱锥P﹣ABCD中,PC与平面ABCD所成角的正切值为 . 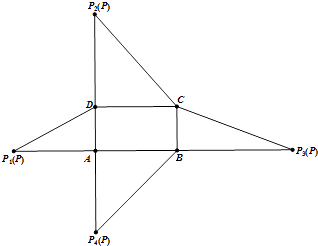
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD= ![]() ,AB=AC.
,AB=AC. 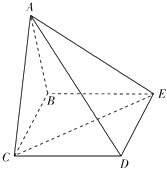
(1)证明:AD⊥CE;
(2)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=2,直线l:y=kx﹣2.
(1)若直线l与圆O交于不同的两点A,B,当 ![]() 时,求k的值;
时,求k的值;
(2)若 ![]() 是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点?若过定点则求出该定点,若不存在则说明理由;
是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,探究:直线CD是否过定点?若过定点则求出该定点,若不存在则说明理由;
(3)若EF、GH为圆O:x2+y2=2的两条相互垂直的弦,垂足为 ![]() ,求四边形EGFH的面积的最大值.
,求四边形EGFH的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( ) 
A.20
B.22.5
C.22.75
D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: 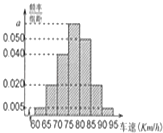
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= ![]() )
)
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() a)的定义域为R;命题q:不等式
a)的定义域为R;命题q:不等式 ![]() <1+ax对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
<1+ax对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com