
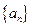 满足:
满足: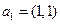 ,
,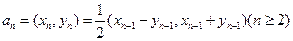
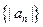 是等比数列;
是等比数列;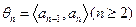 ,
,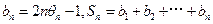 ,求
,求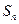 ;
;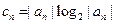 ,问数列
,问数列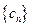 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.科目:高中数学 来源:不详 题型:解答题
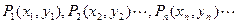 ,对一切正整数
,对一切正整数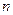 ,点
,点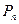 位于函数
位于函数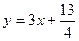 的图象上,且
的图象上,且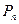 的横坐标构成以
的横坐标构成以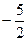 为首项,
为首项,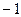 为公差的等差数列
为公差的等差数列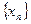 。
。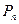 的坐标;
的坐标;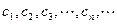 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于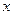 轴,第
轴,第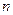 条抛物线
条抛物线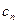 的顶点为
的顶点为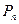 ,且过点
,且过点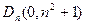 ,记与数列
,记与数列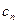 相切于
相切于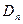 的直线的斜率为
的直线的斜率为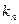 ,求:
,求: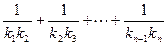 。
。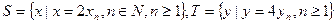 ,等差数列
,等差数列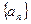 的任一项
的任一项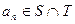 ,其中
,其中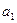 是
是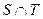 中的最大数,
中的最大数,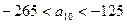 ,求
,求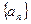 的通项公式。
的通项公式。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
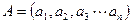 ,
,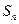 为其前
为其前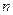 项和,定义
项和,定义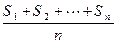 为A的“凯森和”,如果有99项的数列
为A的“凯森和”,如果有99项的数列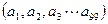 的“凯森和”为1000,则有100项的数列
的“凯森和”为1000,则有100项的数列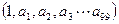 的“凯森和”为( )
的“凯森和”为( )| A.1001 | B.991 | C.999 | D.990 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
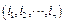 (
(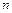 是不小于
是不小于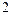 的正整数),如果在
的正整数),如果在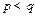 时有
时有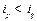 ,则称“
,则称“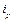 与
与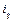 ”是该数组的一个“顺序”,一个数组中所有“顺序”的个数称为此数组的“顺序数”.例如,数组
”是该数组的一个“顺序”,一个数组中所有“顺序”的个数称为此数组的“顺序数”.例如,数组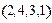 中有顺序“2,4”,“2,3”,其“顺序数”等于2.若各数互不相等的正数数组
中有顺序“2,4”,“2,3”,其“顺序数”等于2.若各数互不相等的正数数组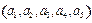 的“顺序数”是4,则
的“顺序数”是4,则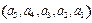 的“顺序数”是 .
的“顺序数”是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
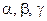 三个字母组成一个长度为
三个字母组成一个长度为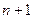
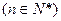 个字母的字符串,要求由
个字母的字符串,要求由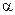 开始,相邻两个字母不同. 例如
开始,相邻两个字母不同. 例如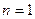 时,排出的字符串可能是
时,排出的字符串可能是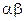 或
或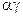 ;
;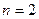 时排出的字符串可能是
时排出的字符串可能是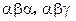
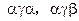 (如图).若记长度为
(如图).若记长度为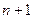 个字母的字符串中,以字母
个字母的字符串中,以字母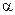 结尾的所有字符串的种数为
结尾的所有字符串的种数为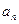 ,
,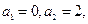 则数列
则数列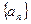 的前
的前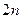 项之和为 .
项之和为 .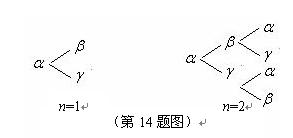
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com