
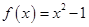 ,设曲线
,设曲线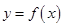 在点
在点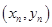 处的切线与
处的切线与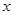 轴的交点为
轴的交点为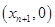 ,其中
,其中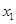 为正实数.
为正实数.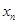 表示
表示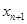 ;
;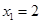 ,若
,若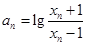 ,试证明数列
,试证明数列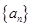 为等比数列,并求数列
为等比数列,并求数列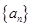 的通项公式;
的通项公式;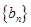 的前
的前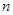 项和
项和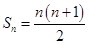 ,记数列
,记数列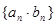 的前
的前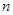 项和
项和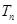 ,求
,求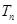 .
.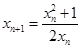 ;(2)证明见解析,
;(2)证明见解析,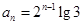 ;(3)
;(3)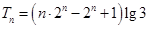 .
.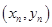 处切线方程,在切线方程中令
处切线方程,在切线方程中令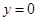 ,就可求出切线与
,就可求出切线与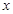 轴交点的横坐标即
轴交点的横坐标即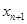 ;(2)要证明数列
;(2)要证明数列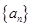 为等比数列,关键是找到
为等比数列,关键是找到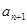 与
与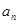 的关系,按题设,它们由
的关系,按题设,它们由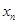 联系起来,
联系起来,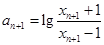 ,把
,把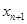 用(1)中的结论
用(1)中的结论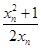 代换,变为
代换,变为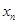 的式子,它应该与
的式子,它应该与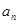 是有联系的,由此就可得出结论;(3)按照要求,首先求出数列
是有联系的,由此就可得出结论;(3)按照要求,首先求出数列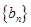 的通项公式,当然要利用
的通项公式,当然要利用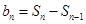 (
(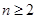 ),
),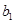 直接等于
直接等于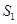 ,数列
,数列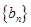 实际上是一个等差数列,那么数列
实际上是一个等差数列,那么数列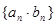 就是由一个等差数列和一个等比数列的对应项相乘得到的新数列,其前
就是由一个等差数列和一个等比数列的对应项相乘得到的新数列,其前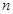 项的求法是乘公比错位相减法,即
项的求法是乘公比错位相减法,即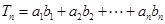 ,记等比数列
,记等比数列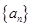 的公比是
的公比是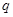 ,则有
,则有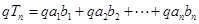
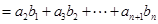 ,两式相减,即
,两式相减,即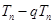 ,这个和是容易求得的.
,这个和是容易求得的.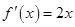 ,所以在曲线上点
,所以在曲线上点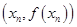 处的切线方程为
处的切线方程为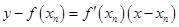 ,即
,即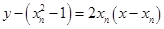
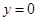 ,得
,得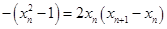 ,即
,即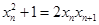
 ,所以
,所以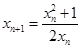 5′
5′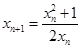 ,所以
,所以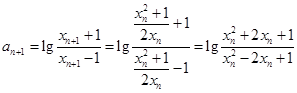
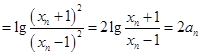 即
即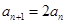 ,
,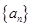 为等比数列故
为等比数列故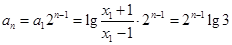 10′
10′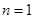 时,
时,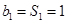 ,当
,当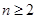 时,
时,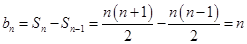
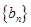 的通项公式为
的通项公式为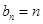 ,故数列
,故数列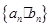 的通项公式为
的通项公式为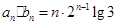
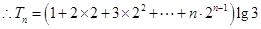 ①
①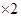 的
的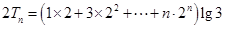 ②
②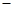 ②得
②得
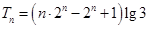 16′
16′

科目:高中数学 来源:不详 题型:单选题
A.(-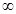 ,-1) ,-1) | B.(-1,0) | C.(0,1) | D.(1,+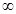 ) ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com