
分析 由题意可得Sn=$\frac{{a}_{n}{a}_{n+1}}{{a}_{n+1}-{a}_{n}}$,再根据递推公式得到an2=an+1an-1,继而得到an=$\left\{\begin{array}{l}{1,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$,再求出前n项和,再根据求和公式求出答案.
解答 解:∵(a1+a2+…+an)an=(a1+a2+…+an-1)an+1=(a1+a2+…+an-1+an-an)an+1=(a1+a2+…+an-1+an)an+1-anan+1,
∴anan+1=(a1+a2+…+an)(an+1-an),
当n=2时,a2a3=(a1+a2)(a3-a2),
∴a3=2,
∴Sn=$\frac{{a}_{n}{a}_{n+1}}{{a}_{n+1}-{a}_{n}}$,
∴Sn-1=$\frac{{a}_{n}{a}_{n-1}}{{a}_{n}-{a}_{n-1}}$,n≥3,
∴an=Sn-Sn-1=$\frac{{a}_{n}{a}_{n+1}}{{a}_{n+1}-{a}_{n}}$-$\frac{{a}_{n}{a}_{n-1}}{{a}_{n}-{a}_{n-1}}$,
整理得an2=an+1an-1,
∴数列{an}从第3项开始为等比数列,
当n=3时,a32=a4a2,∴a4=4,
∴q=$\frac{4}{2}$=2,
∴an=$\left\{\begin{array}{l}{1,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$
当n≥2时,Sn=1+$\frac{1•(1-{2}^{n-1})}{1-2}$=2n-1,
∴Sn=$\left\{\begin{array}{l}{1,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$
当n≥2时,Sn•Sn-1=2n-12n-2=22n-3,
∴S1S2+S2S3+S3S4+…+Sn-1Sn=21+23-+25+…+22n-3=$\frac{2(1-{2}^{2n-3})}{1-4}$=$\frac{{2}^{2n-1}-2}{3}$
故答案为:$\frac{{{2^{2n-1}}-2}}{3}$.
点评 本题考查了数列的递推公式和等比数列的通项公式和前n项和公式,考查了分析问题解决问题的,以及运算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的铁片由两部分组成,半径为1的半圆O及等腰直角△EFH,其中FE⊥FH.现将铁片裁剪成尽可能大的梯形铁片ABCD(不计损耗),AD∥BC,且点A,B在弧$\widehat{EF}$上.点C,D在斜边EH上.设∠AOE=θ.
如图所示的铁片由两部分组成,半径为1的半圆O及等腰直角△EFH,其中FE⊥FH.现将铁片裁剪成尽可能大的梯形铁片ABCD(不计损耗),AD∥BC,且点A,B在弧$\widehat{EF}$上.点C,D在斜边EH上.设∠AOE=θ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
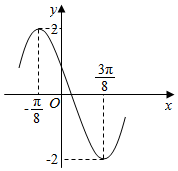 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com