Question

7．如图所示的铁片由两部分组成，半径为1的半圆O及等腰直角△EFH，其中FE⊥FH．现将铁片裁剪成尽可能大的梯形铁片ABCD（不计损耗），AD∥BC，且点A，B在弧$\widehat{EF}$上．点C，D在斜边EH上．设∠AOE=θ．
（1）求梯形铁片ABCD的面积S关于θ的函数关系式；
（2）试确定θ的值，使得梯形铁片ABCD的面积S最大，并求出最大值．

Answer 1

分析 （1）利用含有θ的代数式表示梯形ABCD的上下底面边长和高，代入梯形的面积公式求得ABCD的面积S关于θ的函数关系式；
（2）对得到的面积关于θ的关系式求导，求出函数的极值点，也就是最大值点，则面积的最大值可求．

解答 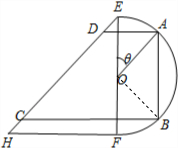解：（1）连接OB，根据对称性可得∠AOE=∠BOF=θ且OA=OB=1，
∴AD=1-cosθ+sinθ，BC=1+cosθ+sinθ，AB=2cosθ，
∴S=$\frac{（AD+BC）•AB}{2}$=2（1+sinθ）cosθ，其中0＜θ＜$\frac{π}{2}$；
（2）记f（θ）=2（1+sinθ）cosθ，其中0＜θ＜$\frac{π}{2}$，
f′（θ）=2（cos²θ-sinθ-sin²θ）=-2（2sinθ-1）（sinθ+1）（0＜θ＜$\frac{π}{2}$）．
当0＜θ＜$\frac{π}{6}$时，f′（θ）＞0，当$\frac{π}{6}$＜θ＜$\frac{π}{2}$时，f′（θ）＜0，
∴θ=$\frac{π}{6}$时，S_max=$\frac{3\sqrt{3}}{2}$．

点评 本题考查了简单的建模思想方法，考查了三角函数最值的求法，训练了利用导数求函数的最值，是中档题．