
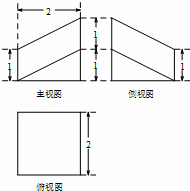
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如
图所示,那么该几何体的体积是( )
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的 名候车乘客中随机抽取
名候车乘客中随机抽取 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成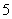 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 | 候车时间 | 人数 |
| 一 |
|
|
| 二 |
|
|
| 三 |
|
|
| 四 |
|
|
| 五 |
|
|
(1)求这 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这 名乘客中候车时间少于
名乘客中候车时间少于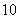 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的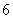 人中选
人中选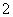 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点P(x,y)在直线x+2y=3上移动,当2x+4y取最小值时,过P点(x,y)引圆C: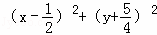 =1的切线,则此切线长等于( )
=1的切线,则此切线长等于( )
|
| A. | 1 | B. |
| C. |
| D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
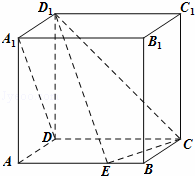
如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是棱AB上的动点.
(Ⅰ)求证:DA1⊥ED1;
(Ⅱ)若直线DA1与平面CED1成角为45°,求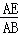 的值;
的值;
(Ⅲ)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数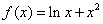 .
.
(I)若函数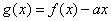 在定义域内为增函数,求实数
在定义域内为增函数,求实数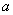 的取值范围;
的取值范围;
(Ⅱ)在(1)的条件下,若 ,
, ,
,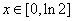 ,求
,求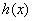 的极小值;
的极小值;
(Ⅲ)设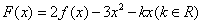 ,若函数
,若函数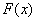 存在两个零点
存在两个零点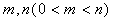 ,
,
且满足 ,问:函数
,问:函数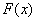 在
在 处的切线能否平行于
处的切线能否平行于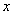 轴?若能,
轴?若能,
求出该切线方程,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn满足2Sn=an+1—2n+l+1,n∈N*,且a1,a2+5,a3成等差数列。
(1)求a1的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com