
向量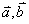 满足
满足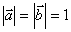 ,
,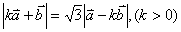 .
.
(1)求 关于k的解析式
关于k的解析式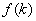 ;
;
(2)请你分别探讨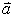 ⊥
⊥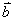 和
和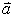 ∥
∥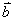 的可能性,若不可能,请说明理由,若可能,求出k的值;
的可能性,若不可能,请说明理由,若可能,求出k的值;
(3)求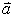 与
与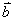 夹角的最大值.
夹角的最大值.
科目:高中数学 来源: 题型:
已知A、B、C是直线l上的三点,O是直线l外一点,向量![]() 满足
满足
![]() =[f(x)+2f ′(1)]
=[f(x)+2f ′(1)] ![]() -ln(x+1)
-ln(x+1)![]()
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>![]() ;
;
(Ⅲ)若不等式![]() x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求函数y=f(x)的表达式;
(2)若g(x)在点(3,g(3))处的切线与直线7x-18y+3=0平行,求函数g(x)的极值;
(3)若函数g(x)在(0,2)上单调递减,求实数a的取值范围.
(文)已知A、B、C是直线l上的三点,且满足:![]() -(y+ax2)
-(y+ax2)![]() +(x3+3x)
+(x3+3x)![]() =0.
=0.
(1)若f(x)在点(1,f(3))处的切线与直线2x+y+3=0平行,求函数y=f(x)的极值;
(2)若函数y=f(x)在(-2,![]() )上单调递减,求实数口的取值范围.
)上单调递减,求实数口的取值范围.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年山东省日照市实验高中高一(下)期末数学练习试卷7(必修3、4)(解析版) 题型:解答题
 满足
满足 ,且
,且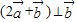
 的坐标;
的坐标;  与
与 的夹角.
的夹角.查看答案和解析>>
科目:高中数学 来源:2009-2010学年四川省遂宁市蓬溪中学实验学校高一(下)第二次月考数学试卷(解析版) 题型:解答题
 满足
满足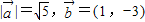 ,且
,且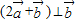
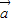 的坐标;
的坐标; 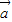 与
与 的夹角.
的夹角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com