
分析 (1)为古典概型,可得总数为4×4=16种,符合题意得为4种,代入古典概型得公式可得;
(2)为几何概型,设甲到达时刻为x,乙到达时刻为y,可得0≤x≤60,0≤y≤60,作出图象由几何概型的公式可得
解答 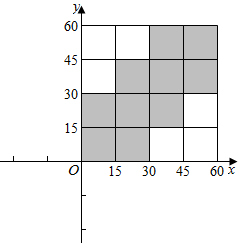 解::(1)他们乘车总的可能结果数为4×4=16种,
解::(1)他们乘车总的可能结果数为4×4=16种,
乘同一班车的可能结果数为4种,
由古典概型知甲乙乘同一班车的概率为P=$\frac{4}{16}=\frac{1}{4}$;
(2)设甲到达时刻为x,乙到达时刻为y,可得0≤x≤60,0≤y≤60,记事件B表示“最多等一辆,且两人同乘一辆车”,
则:B={(x,y)|0≤x≤15,0≤y≤30;15<x≤30,0≤y≤45;30<x≤45,15≤y≤60;45<x≤60,30<y≤60;},如图
概率为$\frac{15×30+15×45+15×45+15×30}{60×60}=\frac{5}{8}$,
故$P(B)=\frac{5}{8}$…(12分)
点评 本题考查几何概型的求解,涉及古典概型,准确作出图象是解决问题的关键,属中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | (¬p)∧(¬q) | C. | p∨(¬q) | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{3}{2}$) | B. | ($\frac{1}{2}$,$\frac{3}{2}$] | C. | ($\frac{1}{2}$,$\frac{3}{2}$) | D. | ($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
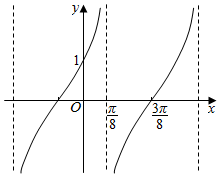 已知函数f(x)=Atan(ωx+φ)$(ω>0,|φ|<\frac{π}{2})$,y=f(x)的部分图象如图,则$f(\frac{π}{24})$=( )π
已知函数f(x)=Atan(ωx+φ)$(ω>0,|φ|<\frac{π}{2})$,y=f(x)的部分图象如图,则$f(\frac{π}{24})$=( )π| A. | 2+$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样 | B. | 抽签法 | C. | 系统抽样 | D. | 分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com