
在△ABC中,角A,B,C所对的边分别为a,b,c,∠B=30°,c=6,记b=f(a),若函数g(a)=f(a)﹣k(k是常数)只有一个零点,则实数k的取值范围是( )
|
| A. | {k|0<k≤3或k=6} | B. | {k|3≤k≤6} | C. | {k|k≥6} | D. | {k|k≥6或k=3} |
考点:
函数零点的判定定理.
专题:
函数的性质及应用.
分析:
由余弦定理可得 b=f(a)的解析式,利用二次函数的性质可得f(a)的最小值为3,f(a)的增区间为[3![]() ,+∞),
,+∞),
减区间为(0,3![]() ),且f(0)趋于6,由此可得实数k的取值范围.
),且f(0)趋于6,由此可得实数k的取值范围.
解答:
解:在△ABC中,∠B=30°,c=6,记b=f(a),
而由余弦定理可得 b=![]() =
=![]()
=![]() ≥3,即f(a)的最小值为3.
≥3,即f(a)的最小值为3.
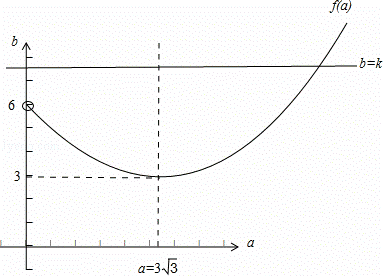
由于函数g(a)=f(a)﹣k(k是常数)只有一个零点,故方函数y=f(a)与直线y=k有唯一交点,
由于函数f(a)的增区间为[3![]() ,+∞),减区间为(0,3
,+∞),减区间为(0,3![]() ),且f(0)趋于6,
),且f(0)趋于6,
结合函数b=f(a)的图象可得 k≥6,或k=3,
故选D.
点评:
本题主要考查函数的零点与方程的根的关系,二次函数的性质应用,体现了转化的数学思想,属于基础题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11 | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| b |
| a |
| sinB |
| cosA |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com