
【题目】若定义在R上的偶函数![]() 满足
满足![]() ,且
,且![]() 时,
时,![]() ,则函数
,则函数![]() 的零点个数是( )
的零点个数是( )
A. 6个B. 8个C. 2个D. 4个
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的三角形ABC中,一机器人从三角形ABC上的每一个顶点移动到另一个顶点,(规定:每次只能从一个顶点移动到另一个顶点),而且按逆时针方向移动的概率为顺时针方向移动的概率的3倍,假设现在机器人的初始位置为顶点A处,则通过三次移动后返回到A处的概率为________________________
查看答案和解析>>
科目:高中数学 来源: 题型:
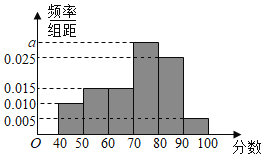
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确命题的序号是____________。
①数列{an}的前n项和![]() ,则数列{ an }是等差数列。
,则数列{ an }是等差数列。
②若等差数列{ an }中,已知![]()
![]()
![]() ,则
,则![]()
![]()
③函数![]() 的最小值为2。
的最小值为2。
④等差数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() 最大时
最大时![]() 13
13
⑤若数列{an}是等比数列,其前n项和为![]() 则常数k的值为1.
则常数k的值为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,原文是:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之. 翻译为现代的语言如下:如果需要对分数进行约分,那么可以折半的话,就折半(也就是用2来约分).如果不可以折半的话,那么就比较分母和分子的大小,用大数减去小数,互相减来减去,一直到减数与差相等为止,用这个相等的数字来约分,现给出“更相减损术”的程序框图如图所示,如果输入的![]() ,
,![]() ,则输出的
,则输出的![]() ( )
( )

A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D为边BC上一点,AD=6,BD=3, DC=2.
(1)若AD⊥BC,求∠BAC的大小;
(2)若∠ABC= ![]() ,求△ADC的面积.
,求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com