考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
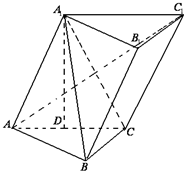
分析:(Ⅰ)由题知A1D⊥平面ABC,从而平面A1ACC1⊥平面ABC,又BC⊥AC,从而BC⊥AC1,由此能证明AC1⊥平面A1BC.
(Ⅱ)法一:建立空间直角坐标系,利用向量法能求出二面角A-A1B-C的余弦值.
(Ⅱ)法二:设A1C∩AC1=O,作OF⊥A1B于F,连AF,则由AO⊥平面A1BC,知AF⊥A1B,∠AFO即是二面角A-A1B-C的平面角,由此能求出二面角A-A1B-C的余弦值.
解答:
(Ⅰ)证明:由题知A
1D⊥平面ABC,而A
1D?平面A
1ACC
1,
所以平面A
1ACC
1⊥平面ABC,…(2分)
又BC⊥AC,BC?平面ABC,
平面A
1ACC
1∩平面ABC=AC,
所以BC⊥平面A
1ACC
1,故BC⊥AC
1,…(4分)
又AC
1⊥A
1B,BC、A
1B?平面A
1BC,BC∩A
1B=B,
所以AC
1⊥平面A
1BC.…(6分)
(Ⅱ)解法一:取AB中点E,连DE,
则由DE、DC、DA
1两两垂直,可如图建立空间直角坐标系,
由(Ⅰ)可知AC
1⊥平面A
1BC,故AC
1⊥A
1C,所以△A
1AC为等边三角形,
所以
A1D=,
故可得各点坐标分别为
A(0 , -1 , 0) , B(2 , 1 , 0) , A1(0 , 0 , ),
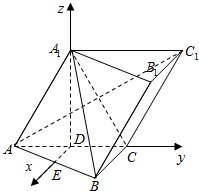 C(0 , 1 , 0) , E(1 , 0 , 0) , C1(0 , 2 , )
C(0 , 1 , 0) , E(1 , 0 , 0) , C1(0 , 2 , )…(9分)
所以
=(2 , 2 , 0),
=(0 , -1 , -) , =(0 , 3 , )设
=(x , y , z)为平面A
1AB的法向量,
则由
,得
,
令x=3,则得
=(3 , -3 , ),…(10分)
又由(Ⅰ)知平面A
1BC的法向量为
=(0 , 3 , ),…(11分)
设所求二面角的大小为θ,则
|cosθ|=|cos? , >|===,…(13分)
因为该二面角为锐角,所以二面角A-A
1B-C的余弦值为
.…(14分)

(Ⅱ)解法二:设A
1C∩AC
1=O,作OF⊥A
1B于F,
连AF,则由AO⊥平面A
1BC,知AF⊥A
1B,
所以∠AFO即是二面角A-A
1B-C的平面角,…(10分)
得
AO=,
OF===,…(11分)
所以
tan∠AFO===,…(13分)
从而二面角A-A
1B-C的余弦值为
.…(14分)
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

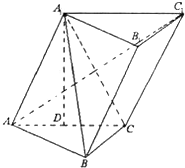 如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D.
如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D. 平面A1ACC1∩平面ABC=AC,
平面A1ACC1∩平面ABC=AC, C(0 , 1 , 0) , E(1 , 0 , 0) , C1(0 , 2 ,
C(0 , 1 , 0) , E(1 , 0 , 0) , C1(0 , 2 , 


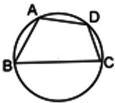 为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.
为了提高校园景观,某校改造花圃用地平面示意图如图所示,经规划调研确定,花圃规划用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原花圃用地,测量可知边界AB=AD=4米,BC=6米,CD=2米.