
【题目】已知椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,左焦点为
,左焦点为![]() ,已知椭圆
,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线与该椭圆
的直线与该椭圆![]() 交于
交于![]() 两点,且线段
两点,且线段![]() 的中点恰为点
的中点恰为点![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由离心率及椭圆过点![]() ,列出关于
,列出关于![]() 的方程求解即可;
的方程求解即可;
(2)设P(xP,yP),Q(xQ,yQ),将两点代入椭圆方程,进而两式作差可得![]() ,进而由点斜式可得解.
,进而由点斜式可得解.
(1)因为e=![]() =
=![]() =
=![]() ,则3a2=4b2,
,则3a2=4b2,
将(1,![]() )代入椭圆方程:
)代入椭圆方程:![]() +
+![]() =1,解得:a=2,b=
=1,解得:a=2,b=![]() ,
,
所以椭圆方程为![]() +
+![]() =1;
=1;
(2)设P(xP,yP),Q(xQ,yQ),
∵线段PQ的中点恰为点N,
∴xP+xQ=2,yP+yQ=2,
∵![]() +
+![]() =1,
=1,![]() +
+![]() =1,两式相减可得
=1,两式相减可得![]() (xP+xQ)(xP﹣xQ)+
(xP+xQ)(xP﹣xQ)+![]() (yP+yQ)(yP﹣yQ)=0,
(yP+yQ)(yP﹣yQ)=0,
∴![]() =﹣
=﹣![]() ,
,
即直线PQ的斜率为﹣![]() ,
,
∴直线PQ的方程为y﹣1=﹣![]() (x﹣1),即3x+4y﹣7=0.
(x﹣1),即3x+4y﹣7=0.


科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P—A1B1C1D1,下部的形状是正四棱柱ABCD—A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
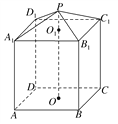
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.
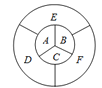
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券2张,每张可获价值50元的奖品;有二等奖券2张,每张可获价值10元的奖品;其余6张没有奖.某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X元的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西光厂眼镜车间接到一批任务,需要加工6000个![]() 型零件和2000个
型零件和2000个![]() 型零件.这个车间有214名工人,他们每一个人加工5个
型零件.这个车间有214名工人,他们每一个人加工5个![]() 型零件的时间可以加工3个
型零件的时间可以加工3个![]() 型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组?
型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com