
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 F(1,0).设A(x1,y1),B(x2,y2).由∠QBF=90°,可得kBFkQB=$\frac{{y}_{2}^{2}}{{x}_{2}^{2}-1}$=-1,又${y}_{2}^{2}=4{x}_{2}$,联立解得x2=$\sqrt{5}$-2.取B$(\sqrt{5}-2,-2\sqrt{\sqrt{5}-2})$,由A,F,B三点共线可得$\frac{{y}_{1}}{{x}_{1}-1}$=$\frac{-2\sqrt{\sqrt{5}-2}}{\sqrt{5}-2-1}$,又${y}_{1}^{2}=4{x}_{1}$,联立解出2.利用|AF|-|BF|=x1-x2即可得出.
解答 解:F(1,0).
设A(x1,y1),B(x2,y2).
∵∠QBF=90°,
∴kBFkQB=$\frac{{y}_{2}}{{x}_{2}-1}$$•\frac{{y}_{2}}{{x}_{2}+1}$=$\frac{{y}_{2}^{2}}{{x}_{2}^{2}-1}$=-1,
又${y}_{2}^{2}=4{x}_{2}$,
∴$\frac{4{x}_{2}}{{x}_{2}^{2}-1}$=-1,化为${x}_{2}^{2}+4{x}_{2}$-1=0,解得x2=$\sqrt{5}$-2.
∴取B$(\sqrt{5}-2,-2\sqrt{\sqrt{5}-2})$,
可得$\frac{{y}_{1}}{{x}_{1}-1}$=$\frac{-2\sqrt{\sqrt{5}-2}}{\sqrt{5}-2-1}$,又${y}_{1}^{2}=4{x}_{1}$,
联立解得x1=$\sqrt{5}$+2.
∴|AF|-|BF|=x1-x2=4.
故选:D.
点评 本题考查了抛物线与圆的标准方程及其性质、相互垂直的直线斜率之间的关系、三点共线与斜率的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
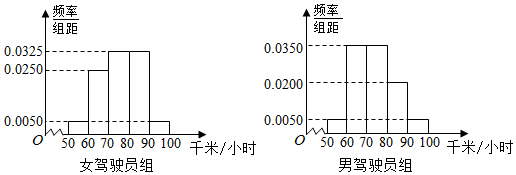
| 危险驾驶 | 非危险驾驶 | 合计 | |
| 男驾驶员 | 15 | 45 | 60 |
| 女驾驶员 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 13 | C. | 15 | D. | 17 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com