
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足 ![]() . (Ⅰ)求角C的值;
. (Ⅰ)求角C的值;
(Ⅱ)若a=5,△ABC的面积为 ![]() ,求sinB的值.
,求sinB的值.
【答案】解:(Ⅰ)由正弦定理, ![]() , 可整理变形为:
, 可整理变形为: ![]() ,
,
由A=π﹣(B+C),可得:sinA=sin(B+C)
所以: ![]() ,
,
整理得: ![]() ,
,
因为sinB≠0,
所以 ![]() ,可得:
,可得: ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
(Ⅱ)由已知a=5, ![]() ,得
,得 ![]() ,
,
由余弦定理得c2=a2+b2﹣2abcosC=21,故 ![]() ,
,
可得: ![]()
【解析】(Ⅰ)由正弦定理,三角函数恒等变换的应用化简已知等式可得 ![]() ,结合sinB≠0,可得:
,结合sinB≠0,可得: ![]() ,进而可求C的值.(Ⅱ)由已知利用三角形面积公式可求b,由余弦定理得c,进而利用正弦定理可求sinB的值.
,进而可求C的值.(Ⅱ)由已知利用三角形面积公式可求b,由余弦定理得c,进而利用正弦定理可求sinB的值.
【考点精析】利用正弦定理的定义和余弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos( ![]() ﹣x)cos(x+
﹣x)cos(x+ ![]() )+
)+ ![]() . (Ⅰ)求函数f(x)的最小正周期和单调递减区间;
. (Ⅰ)求函数f(x)的最小正周期和单调递减区间;
(Ⅱ)求函数f(x)在区间[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= 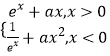 ,若函数f(x)有四个零点,则实数a的取值范围是( )
,若函数f(x)有四个零点,则实数a的取值范围是( )
A.(﹣∞,﹣e)
B.(﹣∞,﹣ ![]() )
)
C.(﹣∞,﹣ ![]() )
)
D.(﹣∞,﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣axlnx(a∈R)在x=1处的切线方程为y=bx+1+
﹣axlnx(a∈R)在x=1处的切线方程为y=bx+1+ ![]() (b∈R).
(b∈R).
(1)求a,b的值;
(2)证明:f(x)< ![]() .
.
(3)若正实数m,n满足mn=1,证明: ![]() +
+ ![]() <2(m+n).
<2(m+n).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的离心率为 ![]() ,F1 , F2分别为椭圆的左右焦点,P为椭圆上任意一点,△PF1F2的周长为
,F1 , F2分别为椭圆的左右焦点,P为椭圆上任意一点,△PF1F2的周长为 ![]() ,直线l:y=kx+m(k≠0)与椭圆C相交于A,B两点. (Ⅰ)求椭圆C的标准方程;
,直线l:y=kx+m(k≠0)与椭圆C相交于A,B两点. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l与圆x2+y2=1相切,过椭圆C的右焦点F2作垂直于x轴的直线,与椭圆相交于M,N两点,与线段AB相交于一点(与A,B不重合).求四边形MANB面积的最大值及取得最大值时直线l的方程;
(Ⅲ)若|AB|=2,试判断直线l与圆x2+y2=1的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mln(x+1),g(x)= ![]() (x>﹣1).
(x>﹣1).
(Ⅰ)讨论函数F(x)=f(x)﹣g(x)在(﹣1,+∞)上的单调性;
(Ⅱ)若y=f(x)与y=g(x)的图象有且仅有一条公切线,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1 , 则双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com