练习册

  • 练习册
  • 试题
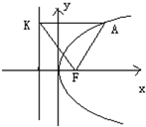
    精英家教网 > 高中数学 > 题目详情
    精英家教网如图，抛物线y2=4x的焦点为F，准线为l，经过F且斜率为
    		3
    的直线与抛物线在x轴上方的部分相交于点A，AK⊥l，垂足为K，则△AKF的面积是
     
    ．
    分析：先判断△AKF为等边三角形，求出A的坐标，可求出等边△AKF的边长AK=m+1的值，△AKF的面积可求．
    解答：解：由抛物线的定义可得AF=AK，∵AF的斜率等于
    		3
    ，∴AF的倾斜角等于60°，∵AK⊥l，
    ∴∠FAK=60°，故△AKF为等边三角形．又焦点F（1，0），AF的方程为 y-0=
    		3
    （x-1），
    设A（m，
    		3
    m-
    		3
    ），m＞1，由AF=AK 得 
    		(m-1)2+(
    		3
    m-
    		3
    )    2
    =m+1，
    ∴m=3，故等边三角形△AKF的边长AK=m+1=4，
    ∴△AKF的面积是
    1
    2
    ×4×4sin60°=4
    		3
    ，
    故答案为4
    		3
    ．
    点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，判断△AKF为等边三角形是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图过抛物线C1：x2=4y的对称轴上一点P（0，m）（m＞0）作直线l与抛物线交于A（x1，y1），B（x2，y2）两点，点Q是P关于原点的对称点，以P，Q为焦点的椭圆为C2．
    （1）求证：x1x2为定值；
    （2）若l的方程为x-2y+4=0，且C1，C2以及直线l有公共点，求C2的方程；
    （3）设
    AP
    =λ
    PB
    ，若
    QP
    ⊥(
    QA
    -μ
    QB
    )    ，求证：λ=μ

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

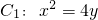    如图过抛物线数学公式的对称轴上一点P（0，m）（m＞0）作直线l与抛物线交于A（x1，y1），B（x2，y2）两点，点Q是P关于原点的对称点，以P，Q为焦点的椭圆为C2．
    （1）求证：x1x2为定值；
    （2）若l的方程为x-2y+4=0，且C1，C2以及直线l有公共点，求C2的方程；
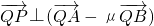    （3）设数学公式，若数学公式，求证：λ=μ

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)的定义域为［0,1］,且满足下列条件:

    ①对于任意x∈［0,1］,总有f(x)≥3,且f(1)=4;

    ②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.

    (1)求f(0)的值;

    (2)求证:f(x)≤4;

    (3)当x∈(］(n=1,2,3,…)时,试证明f(x)＜3x+3.

    (文)如图,设抛物线y2=2px(p＞0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1)、(x2,y2),y1＞0,y2＜0,P是此抛物线的准线上的一点,O是坐标原点.

    (1)求证:y1y2=-p2;

    (2)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;

    (3)若=0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)如图,与抛物线x2=-4y相切于点A(-4,-4)的直线l分别交x轴、y轴于点F、E,过点E作y轴的垂线l0.

    (1)若以l0为一条准线,中心在坐标原点的椭圆恰与直线l也相切,切点为T,求椭圆的方程及点T的坐标;

    (2)若直线l与双曲线6x2-λy2=8的两个交点为M、N,且点A为线段MN的中点,又过点E的直线与该双曲线的两支分别交于P、Q两点,记在x轴正方向上的投影为p,且p2=m,m∈,求(1)中切点T到直线PQ的距离的最小值.

    (文)如图,与抛物线x2=-4y相切于点A(-4,-4)的直线l分别交x轴、y轴于点F、E,过点E作y轴的垂线l0.

    (1)若以l0为一条准线,中心在坐标原点的椭圆恰好过点F,求椭圆的方程;

    (2)若直线l与双曲线6x2-λy2=8的两个交点为M、N,且点A为线段MN的中点,又过点E的直线与该双曲线的两支分别交于P、Q两点,记在x轴正方向上的投影为p,且=m,m∈,求直线PQ的斜率的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江西省上饶市上饶县中学高三（上）期末数学复习试卷3（解析版） 题型：解答题

    如图过抛物线的对称轴上一点P（0，m）（m＞0）作直线l与抛物线交于A（x1，y1），B（x2，y2）两点，点Q是P关于原点的对称点，以P，Q为焦点的椭圆为C2．
    （1）求证：x1x2为定值；
    （2）若l的方程为x-2y+4=0，且C1，C2以及直线l有公共点，求C2的方程；
    （3）设，若，求证：λ=μ

    查看答案和解析>>

    同步练习册答案