
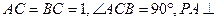 平面ABC,CE//PA,PA=2CE=2。
平面ABC,CE//PA,PA=2CE=2。 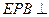 平面APB; (2)求二面角A—BE—P的正弦值。
平面APB; (2)求二面角A—BE—P的正弦值。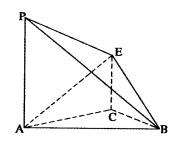
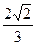
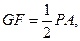 又CE//PA,
又CE//PA,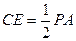 ,
,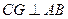 ,又PA
,又PA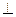 面ABC,得CG
面ABC,得CG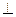 PA,
PA,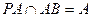 ,
,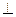 面PAB,因此,EF
面PAB,因此,EF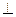 面PAB,又
面PAB,又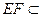 面EPB,
面EPB,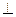 平面APB。
平面APB。 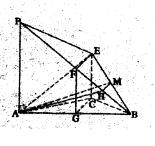 (2)在平面PAB内过点A作AB
(2)在平面PAB内过点A作AB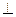 PB于点H,
PB于点H, 平面APB,
平面APB, 平面APB=PB,
平面APB=PB,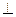 平面EPB,取EB的中点M,
平面EPB,取EB的中点M, MH, 因
MH, 因 为AB=AE=
为AB=AE=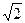 , 所以AM
, 所以AM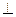 EB,
EB,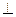 EB,
EB,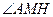 为二面角A—BE—P的平面角。
为二面角A—BE—P的平面角。 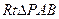 ,PA=2,
,PA=2,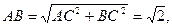
 在
在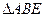 中,AB=BE=EA=
中,AB=BE=EA=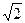 ,
,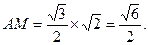
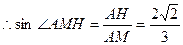
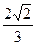


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源:不详 题型:解答题
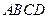 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于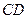 ,线段
,线段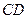 为圆
为圆 的弦,
的弦,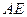 垂直于圆
垂直于圆 所在平面,垂足
所在平面,垂足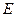 是圆
是圆 上异于
上异于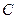 、
、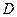 的点,
的点,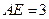 ,圆
,圆 的直径为9.
的直径为9.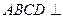 平面
平面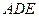 ;
;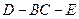 的平面角的正切值.
的平面角的正切值.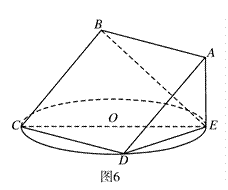
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
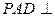 平面ABCD,ABCD为正方形,
平面ABCD,ABCD为正方形,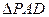 是直角三角形,且
是直角三角形,且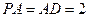 ,E、F、G分别是线段PA,PD,CD的中点.
,E、F、G分别是线段PA,PD,CD的中点.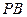 ∥面EFC;
∥面EFC;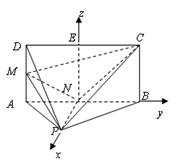
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com