
分析 (1)将圆C方程化成标准形式得(x-2)2+(y+m)2=-m2+2m+3,因此若方程表示圆则-m2+2m+3>0,解之得即可得到实数m的取值范围;
(2)先求出两圆的圆心坐标,再求出两圆圆心连线构成的线段的垂直平分线方程,即为所求.
解答 解:(1)将方程x2+y2-4x+2my+2m2-2m+1=0化成标准形式,得:
(x-2)2+(y+m)2=-m2+2m+3,
∵方程x2+y2-4x+2my+2m2-2m+1=0表示圆C.
∴-m2+2m+3>0,解之得-1<m<3;
(2)由(1)可得-m2+2m+3=4,∴m=1,
∴曲线M的方程为(x-2)2+(y+1)2=4.
直线l是圆x2+y2=4和圆(x-2)2+(y+1)2=4两圆的圆心的垂直平分线,
两圆的圆心分别为N(0,0)、M(2,-1),线段NM的中点 C(1,-$\frac{1}{2}$),
MN的斜率为-$\frac{1}{2}$,故直线l的斜率为2,
由点斜式求得直线l的方程为y+$\frac{1}{2}$=2×(x-1),即4x-2y-3=0.
点评 本题给出含有参数m的圆方程,求参数m的取值范围.着重考查了圆的标准方程和圆与圆的位置关系等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
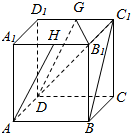 在正方体ABCD-A1B1C1D1中,G是C1D1的中点,H是A1B1的中点
在正方体ABCD-A1B1C1D1中,G是C1D1的中点,H是A1B1的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com