
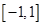 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围; 的值域为区间
的值域为区间 ,且
,且 的长度为
的长度为 的值域为区间
的值域为区间 ,且
,且 的长度为12–q.
的长度为12–q.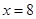 ,∴函数
,∴函数 在区间
在区间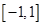 上单调递减,则函数
上单调递减,则函数 在区间
在区间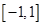 上存在零点须满足
上存在零点须满足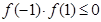 . ……………2分
. ……………2分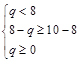 时,即0≤q≤6时,
时,即0≤q≤6时, 的值域为:[f (8),f (q)],即[p–61, q2 –16q + p + 3].
的值域为:[f (8),f (q)],即[p–61, q2 –16q + p + 3].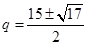 ,经检验
,经检验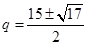 不合题意,舍去.……6分
不合题意,舍去.……6分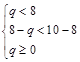 时,即6≤q<8时,
时,即6≤q<8时, 的值域为:
的值域为: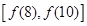 ,即[p – 61,p – 57]
,即[p – 61,p – 57] 的值域为:[f (q),f (10)],即 [q2 – 16q + p +3,p – 57].
的值域为:[f (q),f (10)],即 [q2 – 16q + p +3,p – 57]. 的值域为区间
的值域为区间 ,且
,且 的长度为12–q. ………………………10分
的长度为12–q. ………………………10分

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源:不详 题型:解答题
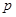 万元和
万元和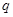 万元,它们与投入资金万元的关系为:
万元,它们与投入资金万元的关系为: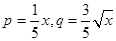 今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少?
今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获得最大利润?最大利润是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com