
(本小题满分12分)定义在 上的函数
上的函数 满足下面三个条件:
满足下面三个条件:
①对任意正数 ,都有
,都有 ;
;
②当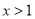 时,
时, ;
;
③ .
.
(1)求 和
和 的值;
的值;
(2)试用单调性定义证明:函数 在
在 上是减函数;
上是减函数;
(3)求满足 的
的 的取值集合.
的取值集合.
(1) ,
, ;(2)略;(3)
;(2)略;(3) .
.
【解析】
试题分析:(1)因为对任意正数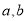 ,都有
,都有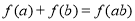 ,所以令
,所以令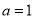 得
得 ,令
,令 得
得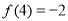 ,令
,令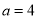 ,
, 得
得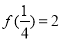 ,对正数
,对正数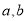 恰当赋值是解此类题目的关键;(2)任取
恰当赋值是解此类题目的关键;(2)任取 ,
, ,且
,且 ,则
,则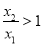 ,
, ,
, ,所以函数
,所以函数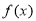 在
在 上是减函数,变形
上是减函数,变形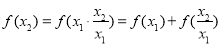 是证明此题的关键;(3)利用(1)中
是证明此题的关键;(3)利用(1)中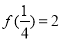 ,(2)中函数
,(2)中函数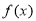 在
在 上是减函数,将
上是减函数,将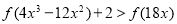 等价变形为
等价变形为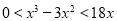 ,解得
,解得 ,这里逆用单调性定义,将函数值之间的关系转化为符合条件的自变量间的关系是解此类问题最基本的方法.
,这里逆用单调性定义,将函数值之间的关系转化为符合条件的自变量间的关系是解此类问题最基本的方法.
试题解析:(1)∵对任意正数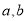 ,都有
,都有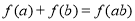 ,∴令
,∴令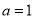 得
得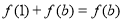 ,
,
∴ , 2分
, 2分
∵ ,∴
,∴ ,
, . 4分(2)任取
. 4分(2)任取 ,
, ,且
,且 , 5分
, 5分
则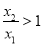 ,∵当
,∵当 时,
时,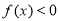 ,∴
,∴ ; 6分
; 6分
∴ 7分
7分
∴函数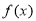 在
在 上是减函数. 8分
上是减函数. 8分
(3)∵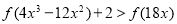 ,∴
,∴ ,解得
,解得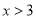 , 9分
, 9分
∴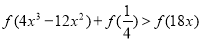 ,即
,即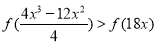 ,亦即
,亦即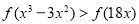 , 10分
, 10分
∴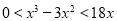 ,解得
,解得 , 11分
, 11分
∴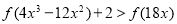 的解集为
的解集为 . 12分
. 12分
考点:①用赋值法求抽象函数的函数值;②抽象函数的单调性的证明;③利用抽象函数的单调性解不等式.


科目:高中数学 来源:2014-2015学年黑龙江省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
在参数方程 (t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )
(t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )
A、 B、
B、 C、
C、 D、
D、
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
已知集合A={x|x2+x-2<0},集合B={x|(x+2)(3-x)>0},则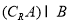 等于( )
等于( )
A. {x|1≤x<3} B. {x|2≤x<3}
C. {x|-2<x<1} D. {x|-2<x≤-1或2≤x<3}
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
如图,在三棱柱ABC—A1B1C1中,AA1⊥面ABC,AC⊥BC,E、F分别在线段 上,B1E=3EC1,AC=BC=CC1=4.
上,B1E=3EC1,AC=BC=CC1=4.

(1)求证:BC⊥AC1;
(2)试探究:在AC上是否存在点F,满足EF//平面A1ABB1,若存在,请指出点F的位置,并给出证明;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二10月定时练习文科数学试卷(解析版) 题型:选择题
设双曲线C的两个焦点为(- ,0),(
,0),( ,0),一个顶点是(1,0),则C的方程为( )
,0),一个顶点是(1,0),则C的方程为( )
A、 B、
B、
C、 D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com