
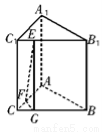
如图,在三棱柱ABC—A1B1C1中,AA1⊥面ABC,AC⊥BC,E、F分别在线段 上,B1E=3EC1,AC=BC=CC1=4.
上,B1E=3EC1,AC=BC=CC1=4.

(1)求证:BC⊥AC1;
(2)试探究:在AC上是否存在点F,满足EF//平面A1ABB1,若存在,请指出点F的位置,并给出证明;若不存在,说明理由.
(1)证明过程详见解析;(2)证明过程详见解析.
【解析】
试题分析:本题主要以三棱柱为几何背景考查线线垂直,线面垂直、线面平行、面面平行等数学知识,考查学生的逻辑推理能力和空间想象能力,考查学生的数形结合思想.第一问,由于AA1⊥面ABC,所以利用线面垂直的性质得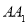 垂直面内的线BC,而
垂直面内的线BC,而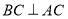 ,利用线面垂直的判定得
,利用线面垂直的判定得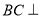 面
面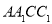 ,所以BC垂直于面
,所以BC垂直于面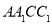 内的线
内的线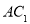 ;第二问,法一:先找到F点的位置,再证明,作出辅助线
;第二问,法一:先找到F点的位置,再证明,作出辅助线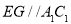 ,因为
,因为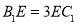 ,所以得到
,所以得到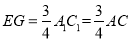 ,而
,而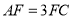 ,即
,即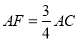 ,所以
,所以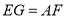 且
且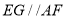 ,所以四边形AFEG为平行四边形,所以
,所以四边形AFEG为平行四边形,所以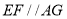 ,所以利用线面平行的判定得
,所以利用线面平行的判定得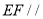 平面
平面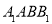 ;法二:作出辅助线
;法二:作出辅助线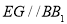 ,利用线面平行的判定,可以推断出
,利用线面平行的判定,可以推断出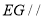 平面
平面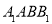 ,
, 平面
平面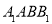 ,利用面面平行的判定,得面
,利用面面平行的判定,得面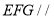 平面
平面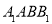 ,所以得
,所以得 平面
平面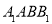 .
.
试题解析:(1)∵AA1⊥面ABC,BC?面ABC,
∴BC⊥AA1.(1分)
又∵BC⊥AC,AA1,AC?面AA1C1C,AA1∩AC=A,∴BC⊥面AA1C1C,(3分)
又AC1?面AA1C1C,∴BC⊥AC1.(4分)
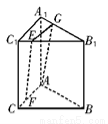
(2)(法一)当AF=3FC时,FE∥平面A1ABB1.(7分)
理由如下:在平面A1B1C1内过E作EG∥A1C1交A1B1于G,连结AG.
∵B1E=3EC1,∴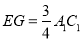 ,
,
又AF∥A1C1且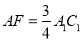 ,
,
∴AF∥EG且AF=EG,
∴四边形AFEG为平行四边形,∴EF∥AG,(10分)
又EF?面A1ABB1,AG?面A1ABB1,∴EF∥平面A1ABB1.(12分)
(法二)当AF=3FC时,FE∥平面A1ABB1.(9分)
理由如下:在平面BCC1B1内过E作EG∥BB1交BC于G,连结FG.
∵EG∥BB1,EG?面A1ABB1,BB1?面A1ABB1,
∴EG∥平面A1ABB1.∵B1E=3EC1,∴BG=3GC,
∴FG∥AB,又AB?面A1ABB1,FG?面A1ABB1,
∴FG∥平面A1ABB1.
又EG?面EFG,FG?面EFG,EG∩FG=G,
∴平面EFG∥平面A1ABB1.(11分)
∵EF?面EFG,∴EF∥平面A1ABB1.(12分)
考点:1. 线线垂直的判定;2.线面垂直的判定;3.线面平行的判定;4.面面平行的判定.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源:2014-2015学年黑龙江省高一上第一次月考数学试卷(解析版) 题型:解答题
(本小题满分12分)定义在 上的函数
上的函数 满足下面三个条件:
满足下面三个条件:
①对任意正数 ,都有
,都有 ;
;
②当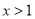 时,
时, ;
;
③ .
.
(1)求 和
和 的值;
的值;
(2)试用单调性定义证明:函数 在
在 上是减函数;
上是减函数;
(3)求满足 的
的 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省高一上第一次月考数学试卷(解析版) 题型:选择题
已知集合A到B的映射 ,那么集合B中象
,那么集合B中象 在A中对应的原象是( )
在A中对应的原象是( )
A.0 B. C.
C.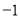 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省哈尔滨市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知 ,
,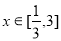 .
.
(1)求 的解析式及定义域;
的解析式及定义域;
(2)若方程 有实数根,求实数
有实数根,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二10月定时练习文科数学试卷(解析版) 题型:解答题
(13分)已知抛物线: ,
,
(1)直线 与抛物线有且仅有一个公共点,求实数
与抛物线有且仅有一个公共点,求实数 的值;
的值;
(2)定点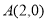 ,P为抛物线上任意一点,求线段长
,P为抛物线上任意一点,求线段长 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:选择题
已知 与
与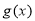 都是定义在R上的函数,
都是定义在R上的函数,  ,且
,且
 ,且
,且 ,在有穷数列
,在有穷数列 中,任意取前
中,任意取前 项相加,则前
项相加,则前 项和大于
项和大于 的概率是( )
的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com