练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    关于x的不等式x2-2ax+a+2≤0的解集为M，如果[1，4]⊆M，则实数a的取值范围为________．

    [3，+∞）
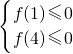
    分析：由已知中关于x的不等式x2-2ax+a+2≤0的解集为M，如果[1，4]⊆M，根据地二次函数的图象和性质，我们易得，解不等式组，即可得到满足条件的实数a的取值范围
    解答：∵不等式x2-2ax+a+2≤0的解集为M，如果[1，4]⊆M，
    令f（x）=x2-2ax+a+2
    ∴
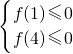
    即
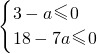
    解得：a≥3
    故实数a的取值范围为[3，+∞）
    故答案为：[3，+∞）
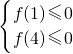
    点评：本题考查的知识点是二次函数的图象，其中根据二次函数的图象分析出[1，4]⊆M时，，将问题转化解不等式组问题，是解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知关于x的不等式x2-（3a+1）x+2a（a+1）＜0的解集是A，函数f(x)=
    1
    2-x
    x+1
    的定义域是B，若A⊆B．求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知不等式x2≤5x-4解集A，关于x的不等式x2-（a+2）x+2a≤0（a∈R）解集为M．
    （1）求集合A；
    （2）若 M⊆A，求实数a的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    关于x的不等式x2-（a+1）x+a＜0的解集中恰有3个整数解，则a的取值范围是
    [-3，-2）∪（4，5]
    [-3，-2）∪（4，5]
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    集合A={ t|t∈Z，关于x的不等式x2≤2-|x-t|至少有一个负数解 }，则集合A中的元素之和等于
    -2
    -2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•重庆）关于x的不等式x2-2ax-8a2＜0（a＞0）的解集为（x1，x2），且：x2-x1=15，则a=（　　）

    查看答案和解析>>

    同步练习册答案