
证明不等式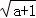 ﹣
﹣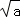 <
<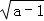 ﹣
﹣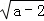 (a≥2)所用的最合适的方法是 .
(a≥2)所用的最合适的方法是 .
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷(解析版) 题型:选择题
用反证法证明命题“如果a>b,那么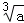 >
>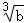 ”时,假设的内容是( )
”时,假设的内容是( )
A.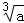 =
=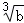 B.
B.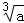 <
<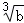
C.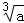 =
=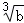 且
且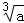 >
>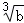 D.
D.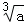 =
=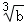 或
或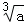 <
<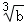
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷(解析版) 题型:选择题
要证 ,只需证
,只需证 +1,即需证
+1,即需证 ,即需证
,即需证 ,即证35>11,因为35>11显然成立,所以原不等式成立.以上证明运用了( )
,即证35>11,因为35>11显然成立,所以原不等式成立.以上证明运用了( )
A.比较法 B.综合法 C.分析法 D.反证法
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷(解析版) 题型:选择题
某同学证明 +
+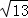 <
<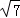 +
+ 的过程如下:∵
的过程如下:∵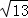 ﹣
﹣ >
>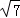 ﹣
﹣ >0,∴
>0,∴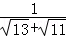 <
<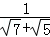 ,∴
,∴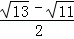 <
<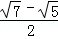 ,∴
,∴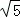 +
+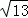 <
<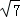 +
+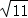 ,则该学生采用的证明方法是( )
,则该学生采用的证明方法是( )
A.综合法 B.比较法 C.反证法 D.分析法
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.1比较法练习卷(解析版) 题型:填空题
(2010•江苏模拟)对于任意的x∈(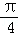 ,
,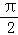 ),不等式psin4x+cos6x≤2sin4x恒成立,则实数p的取值范围为 .
),不等式psin4x+cos6x≤2sin4x恒成立,则实数p的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.1比较法练习卷(解析版) 题型:选择题
已知a=20.5, ,
, ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A.a>c>b B.a>b>c C.c>b>a D.c>a>b
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷(解析版) 题型:选择题
(2014•九江三模)若关于x的不等式|x﹣1|+x≤a无解,则实数a的取值范围是( )
A.(﹣∞,1) B.(﹣∞,1] C.(1,+∞) D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.1不等式练习卷(解析版) 题型:选择题
(2014•兴安盟一模)x、y满足约束条件 ,若目标函数z=ax+by(a>0,b>0)的最大值为7,则
,若目标函数z=ax+by(a>0,b>0)的最大值为7,则 的最小值为( )
的最小值为( )
A.14 B.7 C.18 D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com