
分析 根据分段函数的表达式,分别讨论x的取值范围,利用参数分离法求出a的范围即可得到结论.
解答 解:∵不等式f(x-2)≥f(x)对一切x∈R恒成立,
∴若x≤0,则x-2≤-2.
则不等式f(x-2)≥f(x)等价为,-2(x-2)≥-2x,
即4≥0,此时不等式恒成立,
若0<x≤2,则x-2≤0,
则不等式f(x-2)≥f(x)等价为,-2(x-2)≥ax2+x,
即ax2≤4-3x,
则a≤$\frac{4-3x}{{x}^{2}}$=$\frac{4}{{x}^{2}}$-$\frac{3}{x}$,
设h(x)=$\frac{4}{{x}^{2}}$-$\frac{3}{x}$=4($\frac{1}{x}$-$\frac{3}{8}$)2-$\frac{9}{16}$,
∵0<x≤2,∴$\frac{1}{x}$≥$\frac{1}{2}$,
则h(x)≥-$\frac{1}{2}$,∴此时a≤-$\frac{1}{2}$,
若x>2,则x-2>0,
则f(x-2)≥f(x)等价为,a(x-2)2+(x-2)≥ax2+x,
即4a(1-x)≥2,
∵x>2,∴-x<-2,1-x<-1,
则不等式等价,4a≤$\frac{2}{1-x}$=-$\frac{2}{x-1}$
即2a≤-$\frac{1}{x-1}$
则g(x)=-$\frac{1}{x-1}$在x>2时,为增函数,
∴g(x)>g(2)=-1,
即2a≤-1,则a≤-$\frac{1}{2}$,
故a的最大值为-$\frac{1}{2}$,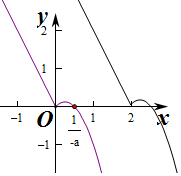
方法2:作出函数f(x)和f(x-2)的图象,
当a≥0时,f(x-2)≥f(x)对一切x∈R不恒成立,
当a<0时,f(x)=-2x,x≤0,f(x-2)=-2(x-2),则f(x-2过定点(2,0),
当x>0时,f(x)=ax2+x的两个零点为x=0和x=-$\frac{1}{a}$,
要使不等式f(x-2)≥f(x)对一切x∈R恒成立,
则只需要-$\frac{1}{a}$≤2,得a≤-$\frac{1}{2}$,
即a的最大值为-$\frac{1}{2}$,
故答案为:-$\frac{1}{2}$
点评 本题主要考查不等式恒成立问题,利用分类讨论的数学思想,结合参数分离法进行求解即可.


科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{\sqrt{2}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2或$\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 7 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤2或x>3} | B. | {x|x≤-2或x>3} | C. | {x|x<2或x≥3} | D. | {x|x<-2或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{11}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
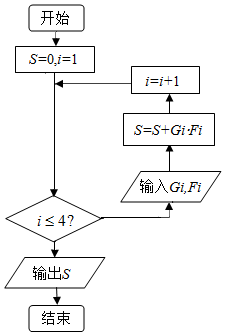 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com