
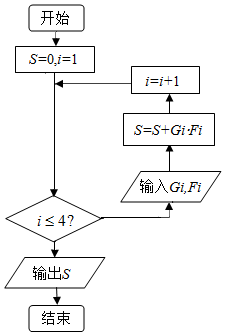
 Ϊ������ѧ���İ�ȫ��ʶ��ij��ѧ������һ�ΰ�ȫ�Ծȵ�֪ʶ�����������800 ��ѧ���μ�����ξ�����Ϊ�˽Ȿ�ξ����ijɼ���������г�ȡ�˲���ѧ���ijɼ����÷־�Ϊ����������Ϊ100 �֣�����ͳ�ƣ��õ����µ�Ƶ�ʷֲ������������Ƶ�ʷֲ�������������⣺
Ϊ������ѧ���İ�ȫ��ʶ��ij��ѧ������һ�ΰ�ȫ�Ծȵ�֪ʶ�����������800 ��ѧ���μ�����ξ�����Ϊ�˽Ȿ�ξ����ijɼ���������г�ȡ�˲���ѧ���ijɼ����÷־�Ϊ����������Ϊ100 �֣�����ͳ�ƣ��õ����µ�Ƶ�ʷֲ������������Ƶ�ʷֲ�������������⣺| ��� ��i�� | ���� �������� | ����ֵ ��Gi�� | Ƶ�� �������� | Ƶ�� ��Fi�� |
| 1 | [60��70�� | 65 | �� | 0.10 |
| 2 | [70��80�� | 75 | 20 | �� |
| 3 | [80��90�� | 85 | �� | 0.20 |
| 4 | [90��100�� | 95 | �� | �� |
| �ϼ� | 50 | 1 | ||
���� ��1���ɷֲ�����Ƶ����Ƶ�ʵĹ�ϵ�����ɵã�
��2������ò�����85�ĸ���P�������������ɵã�
��3���ɵó���Ĺ�������ƽ�������ɱ������ݼ���ɵã�
��� �⣺��1���ɷֲ����ɵ�Ƶ��Ϊ50���ʢٵ���ֵΪ50��0.1=5��
���е�ֵΪ$\frac{20}{50}$=0.40�����е�ֵΪ50��0.2=10��
���е�ֵΪ50-��5+20+10��=15�����е�ֵΪ$\frac{15}{50}$=0.30��
��2��������85�ĸ���P=$\frac{1}{2}$��0.20+0.30=0.40��
���������ԼΪ800��0.40=320��
��3���ó���Ĺ�������ƽ������
S=65��0.10+75��0.40+85��0.20+95��0.30=82��
��800��ѧ����ƽ����Ϊ82��
���� ���⿼��Ƶ�ʷֲ����ͳ����ͼ���������⣮


 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д� �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
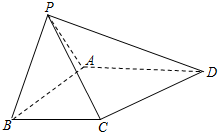 ��ͼ��������P-ABCD�У����������PAB���ڵ�ƽ�������ABCD��ֱ����PBC=��BAD=90�㣮
��ͼ��������P-ABCD�У����������PAB���ڵ�ƽ�������ABCD��ֱ����PBC=��BAD=90�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A+C=2B | B�� | B��B-A��=C��C-A�� | C�� | B2=AC | D�� | B��B-A��=A��C-A�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-1] | B�� | [-1��0] | C�� | [5��+�ޣ� | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | a��c��b | C�� | b��c��a | D�� | c��a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com