
分析 (1)讲曲线C1的极坐标方程两边同乘ρ,根据极坐标与直角坐标的对应关系得到直角坐标方程,先将曲线C2化成普通方程,再化为极坐标方程;
(2)把直线化成直角坐标方程,求出C2的圆心到直线的距离,减去半径即为最小距离.
解答 解:(1)由ρ=2cosθ+2sinθ得,ρ2=2ρcosθ+2ρsinθ,
∴曲线C1的直角坐标方程为x2+y2=2x+2y.
曲线C2的普通方程为(x-2)2+y2=1.即x2+y2-4x+3=0.
∴曲线C2的极坐标方程为ρ2-4ρcosθ+3=0.
(2)曲线C2的圆心为(2,0).
∵ρsin(θ-$\frac{π}{3}$)=3,∴$\frac{1}{2}ρ$sinθ-$\frac{\sqrt{3}}{2}$ρcosθ=3,
直线ρsin(θ-$\frac{π}{3}$)=3的直角坐标方程为$\frac{1}{2}y-\frac{\sqrt{3}}{2}x-3=0$,即$\sqrt{3}$x-y+6=0.
∴曲线C2的圆心到直线的距离为$\frac{2\sqrt{3}+6}{2}$=$\sqrt{3}$+3>1.
∴点P到直线ρsin(θ-$\frac{π}{3}$)=3的最小距离为$\sqrt{3}+$3-1=$\sqrt{3}+2$.
点评 本题考查了极坐标方程,参数方程与普通方程的转化,直线与圆的位置关系,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{\sqrt{2}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2或$\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 7 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
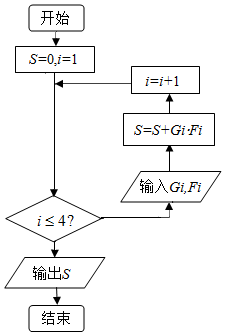 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com