
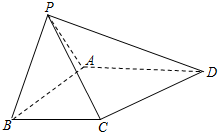
 如图,在四棱锥P-ABCD中,锐角三角形PAB所在的平面与底面ABCD垂直,∠PBC=∠BAD=90°.
如图,在四棱锥P-ABCD中,锐角三角形PAB所在的平面与底面ABCD垂直,∠PBC=∠BAD=90°.分析 (1)在平面PAB内过点P作PH⊥AB于H,由面面垂直的性质可得PH⊥平面ABCD,进而可得PH⊥BC,又可得PB⊥BC,由线面垂直的判定定理可得;
(2)结合题意和(1)的结论易得AD∥BC,由线面平行的判定定理可得.
解答 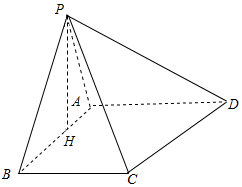 证明:(1)在平面PAB内过点P作PH⊥AB于H,
证明:(1)在平面PAB内过点P作PH⊥AB于H,
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PH?平面PAB,
∴PH⊥平面ABCD,又∵BC?平面ABCD,∴PH⊥BC,
由∠PBC=90°可得PB⊥BC,
又PH∩PB=P,PH,PB?平面PAB,
∴BC⊥平面PAB;
(2)∵AB?平面PAB,∴BC⊥AB,
由∠BAD=90°可得AD⊥AB,
故在平面ABCD中,AD∥BC,
又AD?平面PBC,BC?平面PBC,
∴AD∥平面PBC
点评 本题考查直线和平面平行和垂直的判定,作出辅助线并熟练利用定理是解决问题的关键,属中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 7 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤2或x>3} | B. | {x|x≤-2或x>3} | C. | {x|x<2或x≥3} | D. | {x|x<-2或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{11}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
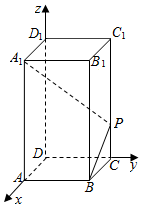 如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在唯一的一点P满足A1P⊥PB,求实数λ的值.
如图,正四棱柱ABCD-A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在唯一的一点P满足A1P⊥PB,求实数λ的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
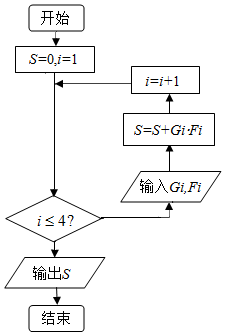 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com