
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据等差数列的性质,分别证明充分性和必要性,从而得到答案.
解答 解:当r=1时,等式an+1=r•an+r化为an+1=an+1,即an+1-an=1(n∈N*).
所以,数列{an}是首项a1=1,公差为1的等差数列;
“r=1”是“数列{an}成等差数列”的充分条件,
当r不等于1时,
由an+1=ran+r=$\frac{{r}^{2}}{r-1}$-$\frac{r}{r-1}$,得an+1+$\frac{r}{r-1}$=r(an+$\frac{r}{r-1}$)
所以,数列{an+$\frac{r}{r-1}$}是首项为$\frac{2r}{r-1}$,公比为r的等比数列
所以,an+$\frac{r}{r-1}$=$\frac{2r}{r-1}$rn-1,
当r=$\frac{1}{2}$时,an=1.{an}是首项为1,公差为0的等差数列.
因此,“r=1”不是“数列{an}成等差数列”的必要条件.
综上可知,“r=1”是“数列{an}成等差数列”的充分但不必要条件.
故选A.
点评 本题考查了必要条件、充分条件及充要条件,解答的关键是判断必要性,也是该题的难点,考查了由递推式求数列的通项公式,对于an+1=pan+q型的递推式,一般都可转化成一个新的等比数列.此题是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{10}}}{3}]$ | B. | $(\frac{{\sqrt{10}}}{3},\frac{{\sqrt{17}}}{3}]$ | C. | $(\frac{{\sqrt{10}}}{3},\sqrt{2}]$ | D. | $(\frac{{\sqrt{17}}}{3},\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
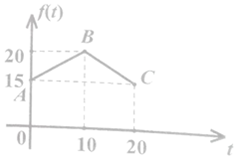 经过市场调查,某门市部的一种小商品在过去的20天内的销售量(件)与价格(元)均为时间t (天)的函数,且日销售量近似满足g(t)=80-2t (件),而日销售量价格近似满足函数f(t),且f(t)的图象为如图所示的两线段AB,BC.
经过市场调查,某门市部的一种小商品在过去的20天内的销售量(件)与价格(元)均为时间t (天)的函数,且日销售量近似满足g(t)=80-2t (件),而日销售量价格近似满足函数f(t),且f(t)的图象为如图所示的两线段AB,BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com