
| A. | $(0,\frac{{\sqrt{10}}}{3}]$ | B. | $(\frac{{\sqrt{10}}}{3},\frac{{\sqrt{17}}}{3}]$ | C. | $(\frac{{\sqrt{10}}}{3},\sqrt{2}]$ | D. | $(\frac{{\sqrt{17}}}{3},\sqrt{2}]$ |
分析 根据题意知,A、B1、P、B2 构成一个矩形,以AB1、AB2 所在直线为坐标轴建立直角坐标系;利用不等式综合知识点来求出|OA|的范围.
解答  解:根据题意知,A、B1、P、B2 构成一个矩形,以AB1、AB2 所在直线为坐标轴建立直角坐标系,如图所示:
解:根据题意知,A、B1、P、B2 构成一个矩形,以AB1、AB2 所在直线为坐标轴建立直角坐标系,如图所示:
设|AB1|=a,|AB2|=b,点O的坐标为(x,y),则点P的坐标为(a,b);
由|$\overrightarrow{O{B}_{1}}$|=|$\overrightarrow{O{B}_{2}}$|=1,得$\left\{\begin{array}{l}{(x-a)^{2}+{y}^{2}=1}\\{{x}^{2}+(y-b)^{2}=1}\end{array}\right.$,则$\left\{\begin{array}{l}{(x-a)^{2}=1-{y}^{2}}\\{(y-b)^{2}=1-{x}^{2}}\end{array}\right.$
∵|$\overrightarrow{OP}$|<$\frac{1}{3}$,∴$(x-a)^{2}+(y-b)^{2}<\frac{1}{9}$,
∴1-y2+1-x2<$\frac{1}{9}$;
∴${x}^{2}+{y}^{2}>\frac{17}{9}$;①
又∵(x-a)2+y2=1;
∴y2=1-(x-a)2≤1;
∴y2≤1;
同理x2≤1;
∴x2+y2≤2 ②,
由①②知$\frac{17}{9}<{x}^{2}+{y}^{2}≤2$;
∵|$\overrightarrow{OA}$|=$\sqrt{{x}^{2}+{y}^{2}}$;
∴$\frac{\sqrt{17}}{3}<|\overrightarrow{OA}|≤\sqrt{2}$.
故选:D
点评 本题考查了构造直角坐标系,平面向量的基本应用,以及不等式综合知识点,属中等偏上题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
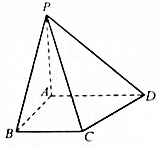 在四棱锥P-ABCD中,四边形ABCD是梯形,AD∥BC
在四棱锥P-ABCD中,四边形ABCD是梯形,AD∥BC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | B. | $\frac{2}{3}$$\overrightarrow{b}$+$\frac{5}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com