
分析 要求三棱锥的体积先找出可以应用的底面和对应的高,这里选择三角形SEF做底面,得到结果.
解答 解:由题意图形折叠为三棱锥,且由S出发的三条棱两两垂直,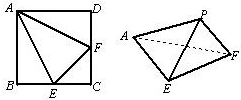
补体为长方体${(2r)^2}={a^2}+{({\frac{a}{2}})^2}+{({\frac{a}{2}})^2},\;\;4{r^2}=\frac{3}{2}{a^2}$,${r^2}=\frac{3}{8}{a^2}$,$r=\frac{{\sqrt{6}}}{4}a$,∴$V=\frac{4}{3}π{r^3}$=$\frac{4}{3}π{({\frac{{\sqrt{6}}}{4}a})^3}=\frac{4}{3}π\;•\;\frac{{6\sqrt{6}}}{4^3}{a^3}=\frac{{\sqrt{6}}}{8}π{a^3}$.
故答案为$\frac{\sqrt{6}}{8}π{a}^{3}$.
点评 本题是基础题,考查几何体的体积的求法,注意折叠问题的处理方法,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{7}{15}$ | C. | $\frac{8}{15}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com