
设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
(1)f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
(2)2
【解析】(1)f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
所以,f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
(2)由于a=1时,(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.
故当x>0时,(x-k)f′(x)+x+1>0等价于
k< +x(x>0) ①
+x(x>0) ①
令g(x)=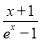 +x,则g′(x)=
+x,则g′(x)= +1=
+1= .
.
由(1)知,函数h(x)=ex-x-2在(0,+∞)上单调递增,
又h(1)=e-3<0,h(2)=e2-4>0.
所以h(x)在(0,+∞)上存在唯一零点.
故g′(x)在(0,+∞)上存在唯一零点.
设此零点为α,则α∈(1,2).
当x∈(0,α)时,g′(x)<0;当x∈(α,+∞)时,g′(x)>0,
所以g(x)在(0,+∞)上的最小值为g(α).
又由g′(α)=0,得eα=α+2, 所以g(α)=α+1∈(2,3).
由于①式等价于k<g(α),
故整数k的最大值为2.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:选择题
设m、n是不同的直线,α、β是不同的平面,下列四个命题中正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥β,n⊥β,则m∥n
C.若α⊥β,m?α,则m⊥β
D.若m?α,n?α,m∥β,n∥β,则α∥β
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(二)(解析版) 题型:选择题
设向量a=(1,x-1),b=(x+1,3),则“x=2”是“a∥b”的( )
A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(三)(解析版) 题型:选择题
已知函数y=f(x)是定义在R上且以3为周期的奇函数,当x∈ 时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
A.3 B.5 C.7 D.9
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(三)(解析版) 题型:选择题
实数x,y满足 ,若目标函数z=x+y取得最大值4,则实数a的值为( )
,若目标函数z=x+y取得最大值4,则实数a的值为( )
A.4 B.3 C.2 D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(一)(解析版) 题型:解答题
设集合A={x|x2<4},B={x|1<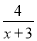 }.
}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(一)(解析版) 题型:选择题
先作函数y=lg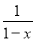 的图象关于原点对称的图象,再将所得图象向右平移一个单位得图象C1,函数y=f(x)的图象C2与C1关于直线y=x对称,则函数y=f(x)的解析式为( )
的图象关于原点对称的图象,再将所得图象向右平移一个单位得图象C1,函数y=f(x)的图象C2与C1关于直线y=x对称,则函数y=f(x)的解析式为( )
A.y=10x B.y=10x-2
C.y=lg x D.y=lg(x-2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入(解析版) 题型:填空题
在?ABCD中, =a,
=a, =b,
=b, =3
=3 ,M为BC的中点,则
,M为BC的中点,则 =______(用a,b表示).
=______(用a,b表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com