
分析 (1)在R上的奇函数,f(0)=0求参数;(2)不等式f(t2-2t)+f(2t2-k)<0恒成立,转化为k<(3t2-2t)min求解.
解答 解:(1)因为f(x)是定义在R上的奇函数,
所以f(0)=0,
所以f(0)=$\frac{-1+b}{2+a}$=0,所以b=1,
因为f(x)=$\frac{-2x+1}{2x+1+a}$,
所以f(-x)=$\frac{-2-x+1}{2-x+1+a}$=$\frac{2x-1}{2+a•2x}$.
因为f(-x)=-f(x),
所以$\frac{2x-1}{2+a•2x}$=$\frac{2x-1}{2x+1+a}$,
所以(2-a)(1-2x)=0,
所以a=2,
所以f(x)=$\frac{-2x+1}{2x+1+2}$.
(2)因为f(t2-2t)+f(2t2-k)<0恒成立,
所以f(t2-2t)<-f(2t2-k)恒成立,
因为f(x)为R上的奇函数,
所以f(t2-2t)<f(-2t2+k)恒成立,
因为函数f(x)在R上单调递减,
所以t2-2t>-2t2+k恒成立,所以k<3t2-2t恒成立,
又因为g(t)=3t2-2t在R上最小值为$\frac{-4}{4×3}=-\frac{1}{3}$
k<-$\frac{1}{3}$.
点评 本题考查了奇函数的性质,不等式恒成立问题的转化,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{5}{2}$) | B. | ($\frac{5}{2}$,+∞) | C. | (-∞,-1) | D. | (6,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y∈(0,1) | B. | y∈(1,2 ) | C. | y∈(2,3 ) | D. | y=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
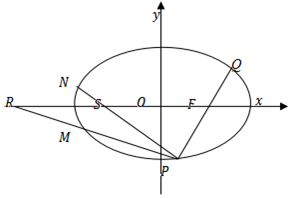 如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.
如图,椭圆C:$\frac{x^2}{9}$+$\frac{y^2}{b^2}$=1(0<b<3)的右焦点为F,P为椭圆上一动点,连接PF交椭圆于Q点,且|PQ|的最小值为$\frac{8}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4种 | B. | 10种 | C. | 12种 | D. | 22种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.
光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.| 第t天 | 10 | 17 | 21 | 30 |
| Q(件) | 180 | 152 | 136 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com