
已知椭圆 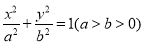 的离心率为
的离心率为  ,且过点
,且过点 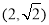
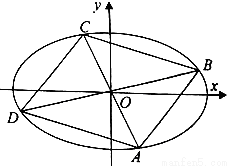
(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形ABCD的顶点在椭圆上,且对角线AC、BD过原点O,若 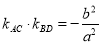 .
.
(i)求  的最值:
的最值:
(i i)求证:四边形ABCD的面积为定值.
(Ⅰ) 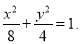 (Ⅱ) (ⅰ)2, (i i)见解析
(Ⅱ) (ⅰ)2, (i i)见解析
【解析】
试题分析:(Ⅰ) 由离心率为 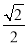 知
知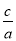 =
=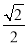 ,将点
,将点 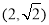 代入椭圆方程,又可得到关于a,b的方程,结合
代入椭圆方程,又可得到关于a,b的方程,结合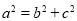 即可求出
即可求出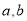 的值,得到椭圆方程;(Ⅱ) (ⅰ)设出点A,B的坐标及直线AB的方程,将直线AB的方程代入椭圆方程,化为关于x的二次方程,利用点A、B的横坐标分别为该二次方程的解,则判别式大于等于0,且利用韦达定理,将横坐标之和和之积用参数表示出来,利用直线的斜率公式将直线OA、OB的斜率用参数表示出来,在利用条件
的值,得到椭圆方程;(Ⅱ) (ⅰ)设出点A,B的坐标及直线AB的方程,将直线AB的方程代入椭圆方程,化为关于x的二次方程,利用点A、B的横坐标分别为该二次方程的解,则判别式大于等于0,且利用韦达定理,将横坐标之和和之积用参数表示出来,利用直线的斜率公式将直线OA、OB的斜率用参数表示出来,在利用条件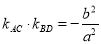 找出参数的关系式,利用向量数量积坐标公式将
找出参数的关系式,利用向量数量积坐标公式将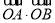 用参数表示出来,将其化为函数的最值问题,利用函数求最值的方法
用参数表示出来,将其化为函数的最值问题,利用函数求最值的方法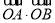 的最值;(i i)由椭圆的对称性知四边形ABCD为平行四边形,故四边形ABCD的面积化为4个△OAB,利用点到直线距离公式距离公式和弦长公式求出△AOB为定值,就证明了四边形ABCD的面积为定值.
的最值;(i i)由椭圆的对称性知四边形ABCD为平行四边形,故四边形ABCD的面积化为4个△OAB,利用点到直线距离公式距离公式和弦长公式求出△AOB为定值,就证明了四边形ABCD的面积为定值.
试题解析:(Ⅰ)由题意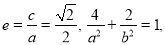 又
又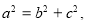
解得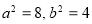 ,故椭圆的标准方程为
,故椭圆的标准方程为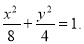 (4分)
(4分)
(Ⅱ)设直线AB的方程为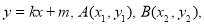
联立 ,得
,得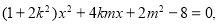
 ①
①

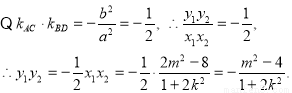
又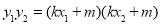 =
=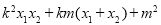 =
=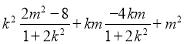 =
=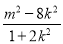 ,
,
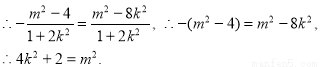 (8分)
(8分)
(ⅰ)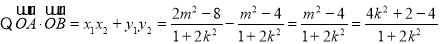
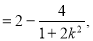

当 (此时
(此时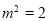 满足①式),即直线AB平行于
满足①式),即直线AB平行于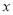 轴时,
轴时,
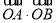 的最小值为-2.
的最小值为-2.
又直线AB的斜率不存在时,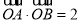 ,∴
,∴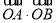 的最大值为2.
的最大值为2.
(ⅱ)设原点到直线AB的距离为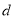 ,则
,则
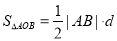 =
=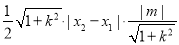 =
=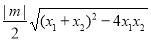
=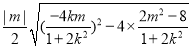 =
=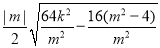 =
=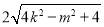 =
=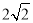 ,
,
∴S四边形ABCD = 4SΔAOB = 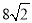 ,
,
即四边形ABCD的面积为定值. .(12分)
考点:椭圆的标准方程与几何性质,直线与椭圆的位置关系,平面向量的数量积,设而不求思想,运算求解能力


科目:高中数学 来源:2013-2014学年河南省长葛市毕业班第三次质量预测(三模)文科数学试卷(解析版) 题型:解答题
某种产品的广告费支出z与销售额y(单位:万元)之间有如下对应数据:

若广告费支出z与销售额y回归直线方程为多一6.5z+n(n∈R).
(1)试预测当广告费支出为12万元时,销售额是多少?
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省郑州市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知直线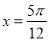 和点
和点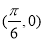 恰好是函数
恰好是函数 的图象的相邻的对称轴和对称中心,则
的图象的相邻的对称轴和对称中心,则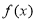 的表达式可以是
的表达式可以是
A.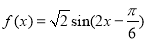 B.
B.
C.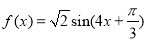 D.
D.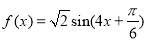
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省毕业班高考适应性模拟练习理科数学试卷(解析版) 题型:选择题
已知直线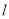 和双曲线
和双曲线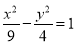 相交于A,B两点,线段AB的中点为M.设直线
相交于A,B两点,线段AB的中点为M.设直线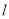 的斜率为k1(k1≠0),直线OM的斜率为k2,则k1k2=( )
的斜率为k1(k1≠0),直线OM的斜率为k2,则k1k2=( )
A. B.-
B.- C.-
C.-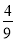 D.
D.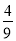
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省毕业班高考适应性模拟练习理科数学试卷(解析版) 题型:选择题
函数 的定义域是( )
的定义域是( )
A.(-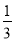 ,1) B.(-
,1) B.(- ,+∞) C.(-
,+∞) C.(- ,
, ) D.(-∞,-
) D.(-∞,-  )
)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试理科数学试卷(解析版) 题型:填空题
已知 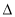 ABC的三个顶点在以O为球心的球面上,且
ABC的三个顶点在以O为球心的球面上,且 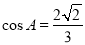 ,BC=1,AC=3,三棱锥O- ABC的体积为
,BC=1,AC=3,三棱锥O- ABC的体积为 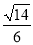 ,则球O的表面积为__________。
,则球O的表面积为__________。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试理科数学试卷(解析版) 题型:选择题
设变量x,y满足约束条件 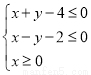 ,则目标函数z=
,则目标函数z=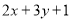 的最大值为
的最大值为
A.11 B.10 C.9 . D.13
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省原名校高三高考仿真模拟统一考试文科数学试卷(解析版) 题型:填空题
已知函数 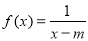 ,若存在
,若存在 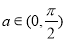 ,使
,使 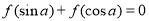 ,则实数m的取值范围是______.
,则实数m的取值范围是______.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
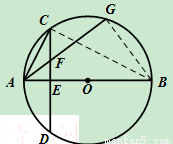
已知, 为圆
为圆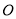 的直径,
的直径,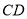 为垂直
为垂直 的一条弦,垂足为
的一条弦,垂足为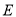 ,弦
,弦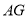 交
交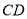 于
于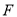 .
.
(1)求证: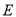 、
、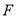 、
、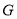 、
、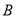 四点共圆;
四点共圆;
(2)若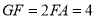 ,求线段
,求线段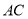 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com