练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知等比数列{an}中，a1+a2+a3=4，a2+a3+a4=-2，则a3+a4+a5+a6+a7+a8=    ．
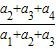
    【答案】分析：先根据q=求出q的值，再根据a3+a4+a5=（a2+a3+a4）•q和a6+a7+a8=（a3+a4+a5）q3，分别求得a3+a4+a5和a6+a7+a8的值，进而求出a3+a4+a5+a6+a7+a8值．
    解答：解：因为q===-，
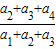
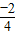
    所以a3+a4+a5=（a2+a3+a4）×（-）=1，
    a6+a7+a8=（a3+a4+a5）×（-）3=，
    于是a3+a4+a5+a6+a7+a8=；
    故答案为：
    点评：本题主要考查了等比数列的性质．本题的关键是利用了a3+a4+a5=（a2+a3+a4）•q和a6+a7+a8=（a3+a4+a5）q3．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    5、已知等比数列{an}的前n项和为Sn，公比q≠1，若S5=3a4+1，S4=2a3+1，则q等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等比数列{an}中，a2=9，a5=243．
    （1）求{an}的通项公式；
    （2）令bn=log3an，求数列{
    1bnbn+1
    }的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等比数列{an}满足a1•a7=3a3a4，则数列{an}的公比q=
    3
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等比数列{an}中a1=64，公比q≠1，且a2，a3，a4分别为某等差数列的第5项，第3项，第2项．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn=log2an，求数列{|bn|}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等比数列{an}中，a3+a6=36，a4+a7=18．若an=
    12
    ，则n=
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案