
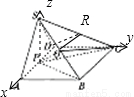
如图,已知四棱锥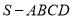 中,
中,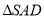 是边长为
是边长为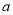 的正三角形,平面
的正三角形,平面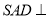 平面
平面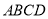 ,四边形
,四边形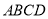 是菱形,
是菱形,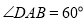 ,
,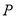 是
是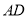 的中点,
的中点,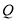 是
是 的中点.
的中点.
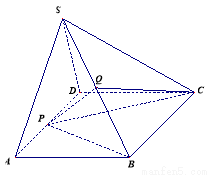
(1)求证: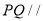 平面
平面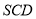 .
.
(2)求二面角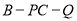 的余弦值.
的余弦值.
(1)取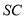 的中点
的中点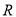 ,连接
,连接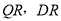 .由题意知
.由题意知 且
且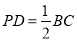 ,
,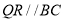 且
且
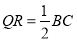 ,所以
,所以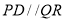 且
且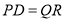 ,即四边形
,即四边形 是平行四边形,所以
是平行四边形,所以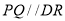 ,
,
又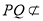 平面
平面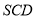 ,
,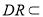 平面
平面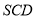 ,所以
,所以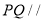 平面
平面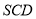 .(2)
.(2)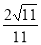 .
.
【解析】
试题分析:(1)取SC中点R,连接QR,DR,根据线面平行的判定定理,在平面上找出一条直线与已知直线平行,即证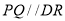 ,从而有
,从而有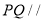 平面
平面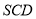 .(2)以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,只要求得两半平面的一个法向量即可,先求得相关点的坐标,进而得到相关向量的坐标,然后用向量的夹角公式求解.
.(2)以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,只要求得两半平面的一个法向量即可,先求得相关点的坐标,进而得到相关向量的坐标,然后用向量的夹角公式求解.
试题解析:(1)取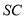 的中点
的中点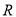 ,连接
,连接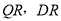 .由题意知
.由题意知 且
且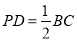 ,
,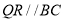 且
且
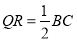 ,所以
,所以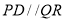 且
且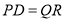 ,即四边形
,即四边形 是平行四边形,所以
是平行四边形,所以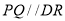 ,
,
又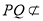 平面
平面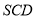 ,
,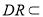 平面
平面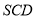 ,所以
,所以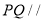 平面
平面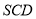 .
.
(2)以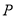 为坐标原点,
为坐标原点,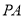 为
为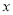 轴,
轴,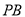 为
为 轴,
轴,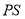 为
为 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,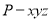 ,则
,则
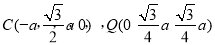 ,平面
,平面 的法向量
的法向量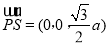 ,设
,设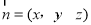 是平面
是平面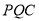 的法向量,
的法向量,
由 ,令
,令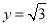 ,得
,得
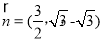 ,
,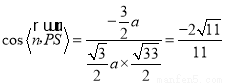
又二面角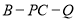 的平面角是锐角,所以二面角
的平面角是锐角,所以二面角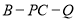 的平面角的余弦值是
的平面角的余弦值是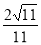 .
.
考点:直线与平面平行的判定;用空间向量求空间的角;二面角的平面角的求法.


科目:高中数学 来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知命题p: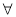 x∈R,x2+x-6
x∈R,x2+x-6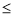 0,则命题
0,则命题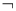 P是( )
P是( )
A.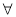 x∈R,x2+x-6>0 B.
x∈R,x2+x-6>0 B.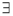 x∈R.x2+x-6>0
x∈R.x2+x-6>0
C.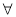 x∈R,x2+x-6>0 D.
x∈R,x2+x-6>0 D.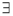 x∈R.x2+x-6<0
x∈R.x2+x-6<0
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
用1,2,3,4,5组成没有重复数字的五位数,其中有且仅有一个偶数夹在两个奇数之间的五位数的个数为
A.36 B.48 C.72 D.120
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
已知x,y的取值如下表所示,若y与x线性相关,且
x | 0 | 1 | 3 | 4 |
| 2.2 | 4.3 | 4.8 | 6.7 |
A.2.2 B.2.6 C.2.8 D.2.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com