
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角
![]() 的余弦值.
的余弦值.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,先根据三角形中位线定理及平行四边形的性质可得
,先根据三角形中位线定理及平行四边形的性质可得![]() ,再证明
,再证明![]() 平面
平面![]() ,从而可得
,从而可得![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果
的一个法向量,根据空间向量夹角余弦公式,可得结果
试题解析:(1)证明:连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() .
.
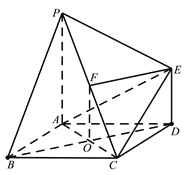
因为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
因为![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]() .
.
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是菱形,所以
是菱形,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解法:因为直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
所以![]() ,所以
,所以![]() .
.
 所以
所以 ![]() ,故△
,故△![]() 为等边三角形.
为等边三角形.
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() .
.
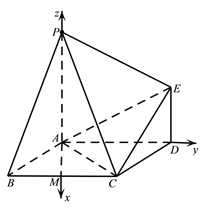
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() (如图).
(如图).
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 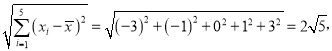 .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() 即
即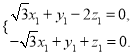
![]() 则
则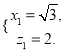 所以
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() 即
即 令
令![]() 则
则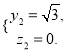 所以
所以![]() .
.
设二面角![]() 的大小为
的大小为![]() ,由于
,由于![]() 为钝角,
为钝角,
所以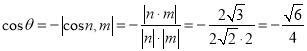 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面垂直及面面垂直的判定定理以及利用空间向量求二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】脐橙营养丰富,含有人体所必需的各类营养成份,若规定单个脐橙重量(单位:千克)在[0.1,0.3)的脐橙是“普通果”,重量在[0.3,0.5)的磨橙是“精品果”,重量在[0.5,0.7]的脐橙是“特级果”,有一果农今年种植脐橙,大获丰收为了了解脐橙的品质,随机摘取100个脐橙进行检测,其重量分别在[0.1,0.2),[0.2,0.3),[0.3,0.4),[0.4,0.5),[0.5,0.6),[0.6,0.7]中,经统计得到如图所示频率分布直方图
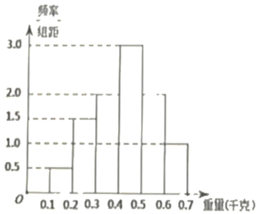
(1)将频率视为概率,用样本估计总体.现有一名消费者从脐橙果园中,随机摘取5个脐橙,求恰有3个是“精品果”的概率.
(2)现从摘取的100个脐橙中,采用分层抽样的方式从重量为[0.4,0.5),[0.5,0.6)的脐橙中随机抽取10个,再从这10个抽取3个,记随机变量X表示重量在[0.5,0.6)内的脐橙个数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四种说法:
(1)函数![]()
![]() 与函数
与函数![]()
![]() 的定义域相同;
的定义域相同;
(2)函数![]() 与
与![]() 的值域相同;
的值域相同;
(3)若函数![]() 式定义在R上的偶函数且在
式定义在R上的偶函数且在![]() 为减函数对于锐角
为减函数对于锐角![]() 则
则![]() ;
;
(4)若函数![]() 且
且![]()
![]() ,则
,则![]() ;
;
其中正确说法的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x,g(x)=x-4,则下列结论正确的是( )
A.若h(x)=f(x)g(x),则函数h(x)的最小值为4
B.若h(x)=f(x)|g(x)|,则函数h(x)的值域为R
C.若h(x)=|f(x)|-|g(x)|,则函数h(x)有且仅有一个零点
D.若h(x)=|f(x)|-|g(x)|,则|h(x)|≤4恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(l)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知直线![]() 分别与曲线
分别与曲线![]() 、曲线
、曲线![]() 交异于极点的
交异于极点的![]() ,若
,若![]() 的极径分别为
的极径分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为回馈顾客,新华都购物商场拟通过摸球兑奖的方式对500位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球(球的大小、形状一模一样),球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为40元,其余3个所标的面值均为20元,求顾客所获的奖励额![]() 的分布列及数学期望;
的分布列及数学期望;
(2)商场对奖励总额的预算是30000元,并规定袋中的4个球由标有面值为20元和40元的两种球共同组成,或标有面值为15元和45元的两种球共同组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的4个球的面值给出一个合适的设计,并说明理由.
提示:袋中的4个球由标有面值为a元和b元的两种球共同组成,即袋中的4个球所标的面值“既有a元又有b元”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
(1)求四棱锥P﹣ABCD的体积;
(2)若E为PC中点,求证:PA∥平面BDE;
(3)求直线PB与平面ABCD所成角的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房产中介公司2017年9月1日正式开业,现对其每个月的二手房成交量进行统计,![]() 表示开业第
表示开业第![]() 个月的二手房成交量,得到统计表格如下:
个月的二手房成交量,得到统计表格如下:

(1)统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() ,如果
,如果![]() ,那么相关性很强;如果
,那么相关性很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱.通过散点图初步分析可用线性回归模型拟合
,那么相关性较弱.通过散点图初步分析可用线性回归模型拟合![]() 与
与![]() 的关系.计算
的关系.计算![]() 的相关系数
的相关系数![]() ,并回答是否可以认为两个变量具有很强的线性相关关系(计算结果精确到0.01)
,并回答是否可以认为两个变量具有很强的线性相关关系(计算结果精确到0.01)
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (计算结果精确到0.01),并预测该房产中介公司2018年6月份的二手房成交量(计算结果四舍五入取整数).
(计算结果精确到0.01),并预测该房产中介公司2018年6月份的二手房成交量(计算结果四舍五入取整数).
(3)该房产中介为增加业绩,决定针对二手房成交客户开展抽奖活动.若抽中“一等奖”获6千元奖金;抽中“二等奖”获3千元奖金;抽中“祝您平安”,则没有奖金.已知一次抽奖活动中获得“一等奖”的概率为![]() ,获得“二等奖”的概率为
,获得“二等奖”的概率为![]() ,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额
,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额![]() (千元)的分布列及数学期望.
(千元)的分布列及数学期望.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的定义域为
的定义域为![]() ,满足对任意
,满足对任意![]() ,有
,有![]() .则称
.则称![]() 为“
为“![]() 形函数”;若函数
形函数”;若函数![]() 定义域为
定义域为![]() ,
,![]() 恒大于0,且对任意
恒大于0,且对任意![]() ,恒有
,恒有![]() ,则称
,则称![]() 为“对数
为“对数![]() 形函数”.
形函数”.
(1)当![]() 时,判断
时,判断![]() 是否是“
是否是“![]() 形函数”,并说明理由;
形函数”,并说明理由;
(2)当![]() 时,判断
时,判断![]() 是否是“对数
是否是“对数![]() 形函数”,并说明理由;
形函数”,并说明理由;
(3)若函数![]() 是
是![]() 形函数,且满足对任意
形函数,且满足对任意![]() 都有
都有![]() ,问
,问![]() 是否是“对数
是否是“对数![]() 形函数”?请加以证明,如果不是,请说明理由.
形函数”?请加以证明,如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com