《环境空气质量指标（
）技术规定（试行）》如表1：
表1：空气质量指标
分组表
表2是长沙市某气象观测点在某连续4天里的记录，指数
与当天的空气水平可见度
的情况.
表2：
表3是某气象观测点记录的长沙市2016年1月1日至1月30日指数频数统计表.
表3：
（1）设
，根据表2的数据，求出
关于
的回归方程；
（2）小李在长沙市开了一家小洗车店，经小李统计：指数不高于200时，洗车店平均每天亏损约200元；指数在200至400时，洗车店平均每天收入约400元；指数大于400时，洗车店平均每天收入约700元.
（ⅰ）计算小李的洗车店在当年1月份每天收入的数学期望.
（ⅱ）若将频率看成概率，求小李在连续三天里洗车店的总收入不低于1200元的概率.（用最小二乘法求线性回归方程系数公式
，
.）
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源：2016届湖南省长沙市高考模拟一文科数学试卷（解析版） 题型：解答题
已知平面直角坐标系
，以
为极点，
轴的非负半轴为极轴建立极坐标系，
点的极坐标为
，曲线
的参数方程为
（
为参数）.
（1）写出点
的直角坐标及曲线
的直角坐标方程；
（2）若
为曲线
上的动点，求
中点
到直线
的距离的最小值.
查看答案和解析>>
科目：高中数学 来源：2016届湖南省长沙市高考模拟一文科数学试卷（解析版） 题型：选择题
执行如图所示的程序框图，输出的结果为98，则判断框内可填入的条件为（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2016届湖南省长沙市高考模拟一理科数学试卷（解析版） 题型：解答题
已知曲线
的极坐标方程是
，以极点为平面直角坐标系的原点，极轴为
轴的正半轴，建立平面直角坐标系，直线
的参数方程是
（
是参数）.
（1）将曲线
的极坐标方程化为直角坐标方程；
（2）若直线
与曲线
相交于
两点，且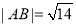
，求直线的倾斜角
的值.
查看答案和解析>>
科目：高中数学 来源：2016届湖南省长沙市高考模拟一理科数学试卷（解析版） 题型：选择题
长郡中学早上8点开始上课，若学生小典与小方均在早上7:40至8:00之间到校，且两人在该时间段的任何时刻到校都是等可能的，则小典比小方至少早5分钟到校的概率为（ ）
A．
B．
C．
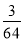D．
查看答案和解析>>
科目：高中数学 来源：2016届云南省高考复习质量监测六文科数学试卷（解析版） 题型：选择题
已知定义在
上的函数
的导函数为
，且对于任意的
，都有
，则下列结论正确的是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2016届海南省高考模拟十文科数学试卷（解析版） 题型：解答题
某河流上的一座水力发电站，每年六月份的发电量
（单位：玩千瓦时）与该河上游在六月份的降雨量
（单位：毫米）有关.据统计，当
时，
每增加10，
增加5.已知近20年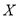
的值为：140,110,160,70,200,160,140,160,220,110,160,160,200,140,110,160,220,140,160.
（1）完成如下的频率分布表：
近20年六月份降雨量频率分布表
（2）假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同，并将频率视为概率，求今年六月份该水力发电站的发电量低于490（万千瓦时）或超过530（万千瓦时）的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的内角
的对边分别为
, 
;
，求角C．
，
，若
是
的充分不必要条件，则实数
的取值范围为 .