练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}是各项均为正数的等比数列，且公比q＜1，则4a5－3a3与a1的大小关系是__________．


    4a5－3a3＜a1


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知{an}是等差数列，公差为d，首项a1＝3，前n项和为Sn.令cn＝(－1)nSn(n∈N*)，{cn}的前20项和T20＝330.数列{bn}满足bn＝2(a－2)dn－2＋2n－1，a∈R.

    (1)求数列{an}的通项公式；

    (2)若bn＋1≤bn，n∈N*，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面中的三角形和空间中的四面体有很多相类似的性质，例如在三角形中，(1)三角形两边之和大于第三边；(2)三角形的面积S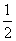＝×底×高；(3)三角形的中位线平行于第三边且等于第三边的；…

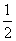    请类比上述性质，写出空间中四面体的相关结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于不等式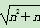<n＋1(n∈N*)，某同学用数学归纳法的证明过程如下：

    (1)当n＝1时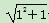，<1＋1，不等式成立．

    (2)假设当n＝k(k∈N*且k≥1)时，不等式成立，即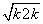<k＋1，则当n＝k＋1时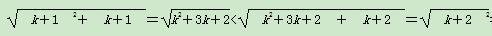，＝(k＋1)＋1，

    所以当n＝k＋1时，不等式成立，则上述证法(　　)

    A．过程全部正确

    B．n＝1验得不正确

    C．归纳假设不正确

    D．从n＝k到n＝k＋1的推理不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a<0，－1<b<0，那么下列不等式成立的是(　　)

    A．a>ab>ab2                             B．ab2>ab>a

    C．ab>a>ab2                             D．ab>ab2>a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列条件：①1<a<b；②0<a<b<1；③0<a<1<b.其中，能推出logb<loga<logab成立的条件的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝－x2＋ax＋b2－b＋1(a∈R，b∈R)，对任意实数x都有f(1－x)＝f(1＋x)成立，当x∈[－1,1]时，f(x)>0恒成立，则b的取值范围是(　　)

    A．－1<b<0                              B．b>2

    C．b<－1或b>2                          D．不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若x，y满足则z＝x＋y的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面直角坐标系中直线y＝2x＋1关于点(1,1)对称的直线方程是(　　)

    A．y＝2x－1                             B．y＝－2x＋1

    C．y＝－2x＋3                           D．y＝2x－3

    查看答案和解析>>

    同步练习册答案