
【题目】已知函数![]() .
.
(1)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(2)![]() ,
,![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;(2)
上单调递增;(2)![]() .
.
【解析】
(1)求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)先利用判别式
的减区间;(2)先利用判别式![]() ,整理得
,整理得![]() ,
,![]() 成立,
成立,![]() ,两次求导可得
,两次求导可得![]() ,由此
,由此![]() ,从而可得结果.
,从而可得结果.
(1)因为![]() ,
,
所以![]() .
.
①当![]() 时,
时,![]() 恒成立,所以函数
恒成立,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上所述,
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
(2)由![]() 得,
得,
![]() ,
,
整理得![]() ,
,
由题意得“![]() ,
,![]() ,总有
,总有![]() 成立”等价于
成立”等价于![]() “,
“,![]() ,
,![]() 恒成立”.
恒成立”.
所以![]() ,
,
方法一:整理得![]() ,
,![]() 成立.
成立.
令![]() ,
,
则![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以![]() ,
,
即![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.
方法二:整理得![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以![]()
即![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)求函数![]() 的定义域,并求出当
的定义域,并求出当![]() 时,常数
时,常数![]() 的值;
的值;
(2)在(1)的条件下,判断函数![]() 在
在![]() 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)设![]() ,若方程
,若方程![]() 有实根,求
有实根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,若an2﹣an﹣12=p,(n≥2,n∈N*,p为常数),则称{an}为“等方差数列”,下列是对“等方差数列“的判断:
①若{an}是等方差数列,则{an2}是等差数列;
②{(﹣1)n}是等方差数列;
③若{an}是等方差数列,则{akn}(k∈N*,k为常数)也是等方差数列;
④若{an}既是等方差数列,又是等差数列,则该数列为常数列.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造.根据史书的记载和考古材料的发现,古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为![]() ,径粗
,径粗![]() ,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“
,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,大约二百七十几枚为一束,放在一个布袋里,系在腰部随身携带.需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄.在算筹计数法中,以纵横两种排列方式来表示数字.如图,是利用算筹表示数1~9的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
”,现有6根算筹,据此表示方法,若算筹不能剩余,则用这6根算筹能表示的两位数的个数为( )
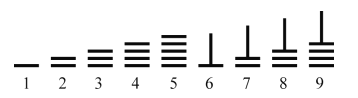
A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知递增数列{an}前n项和为Sn,且满足a1=3,4Sn﹣4n+1=an2,设bn![]() (n∈N*)且数列{bn}的前n项和为Tn
(n∈N*)且数列{bn}的前n项和为Tn
(Ⅰ)求证:数列{an}为等差数列;
(Ⅱ)若对任意的n∈N*,不等式λTn![]() n
n![]() (﹣1)n+1恒成立,求实数λ的取值范围.
(﹣1)n+1恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位响应党中央“精准扶贫”号召,对某村6户贫困户中的甲户进行定点帮扶,每年跟踪调查统计一次,从2015年1月1日至2018年12月底统计数据如下(人均年纯收入):
年份 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 |
收入 | 25 | 28 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
(2)2019年初,根据扶贫办的统计知,该村剩余5户贫困户中还有2户没有脱贫,现从这5户中抽取2户,求至少有一户没有脱贫的概率.
参考公式: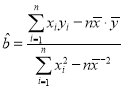 ,
,![]() ,其中
,其中![]() ,
,![]() 为数
为数![]() ,
,![]() 的平均数.
的平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com