练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．若关于x的方程logax=-|x-2|，恰有二个实根，则a的取值范围是（0，1）．

    分析 由题意可得函数y=logax和y=-|x-2|的图象有两个交点．作出函数函数y=logax和y=-|x-2|的图象，对a＞1，0＜a＜1讨论，结合数形结合的思想方法，即可得到所求a的范围．

    解答 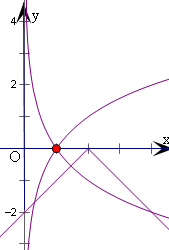解：若关于x的方程logax=-|x-2|，恰有二个实根，
    则函数y=logax和y=-|x-2|的图象有两个交点．
    作出函数函数y=logax和y=-|x-2|的图象，
    当a＞1时，函数y=logax和y=-|x-2|的图象有一个交点；
    当0＜a＜1时，函数y=logax和y=-|x-2|的图象有两个交点．
    故答案为：（0，1）．

    点评 本题考查函数和方程的转化思想的运用，注意运用分类讨论的思想方法，运用数形结合的思想方法是解题的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知双曲线$\frac{x^2}{4}$-$\frac{y^2}{b^2}$=1（b∈N+）的两个焦点分别为F1，F2，P为双曲线上一点，|OP|＜5，若|PF1|，|F1F2|，|PF2|成等比数列，则双曲线的方程为（　　）
    A．$\frac{x^2}{4}$-y2=1B．$\frac{x^2}{4}$-$\frac{y^2}{2}$=1C．$\frac{x^2}{4}$-$\frac{y^2}{3}$=1D．$\frac{x^2}{4}$-$\frac{y^2}{4}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设函数y=f （x），对任意实数x，y都有f （x+y）=f （x）+f （y）+2xy．
    （1）求f （0）的值；
    （2）若f （1）=1，求f （2），f （3），f （4）的值；
    （3）在（2）的条件下，猜想f （n）（n∈N*）的表达式并用数学归纳法证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知集合M={1，3，5，7，9}，N={2，4，6}，下列说法错误的是（　　）
    A．∅=M∩NB．∅⊆M∪NC．∅∈M∩ND．∅∈{M∩N}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．为了解2400名学生的学习情况，计划采用系统抽样的方法从全体学生中抽取容量为100的样本，则分段间隔为24．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知集合A={x|x=3n+1，n∈N}，B={4，6，8，10，12}，则集合A∩B中的元素个数（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．设集合A={x|x2-3x+2=0}，B={x|x2-ax+2=0}，若AUB=A，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．设数列{an}的通项公式为an=n2+bn，若数列{an}是单调递增数列，则实数b的取值范围为（-3，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

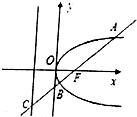    14．如图，已知抛物线y2=4x的焦点为F，过F的直线AB交抛物线于A、B，交抛物线的准线于点C，若$\frac{{|{BF}|}}{{|{BC}|}}$=$\frac{1}{2}$，则|AB|=$\frac{16}{3}$．

    查看答案和解析>>

    同步练习册答案